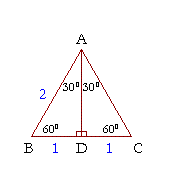
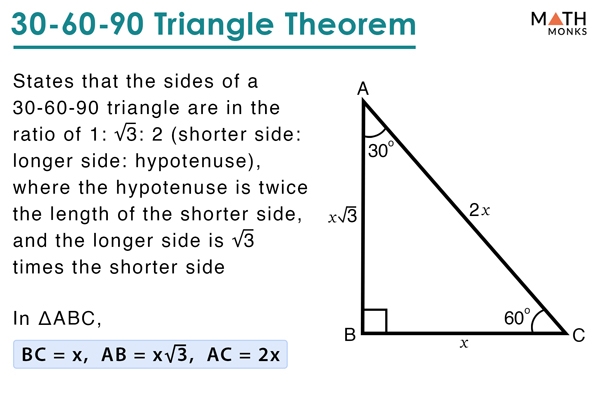
Definition of Triangles The theorem is sum of two any sides of triangles is more than the third side If there are a, b, and c as the sides, then 2 Another special triangle is triangle that has angle 30°, 60°, and 90° It also has ratio in the sides Definition of a triangle along with the ratio of its sidesClick card to see definition 👆 Tap card to see definition 👆 In a 30 60 90 triangle, the hypotenuse is twice as long as the shorter leg, and the longer leg is √3 times as long as the shorter leg Hypotenuse=2x Longer leg= √3 •x Shorter leg=x
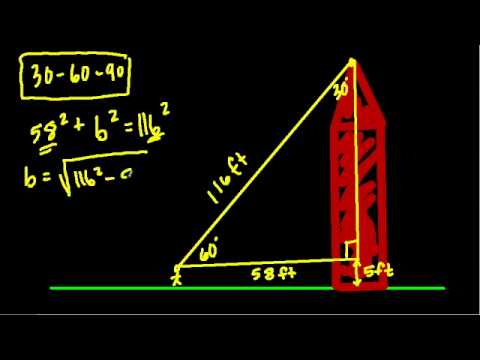
Applying The 30 60 90 Triangle To Height Youtube
Definition of 30 60 90 triangle theorem
Definition of 30 60 90 triangle theorem- Draw an equilateral triangle all sides are equal and the angles are all 60 deg From any angle drop a line perpendicular to the base(an altitude) By triangle congruence laws you can prove the 2 resulting triangles are congruent which means the alTriangle Theorem Problems 100 What is the definition of a degree triangle 100 The acute angles of a right triangle are complementary, so the measure of the third angle is 90 and another is 45 One leg length is 10 units Find the length of the hypotenuse



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
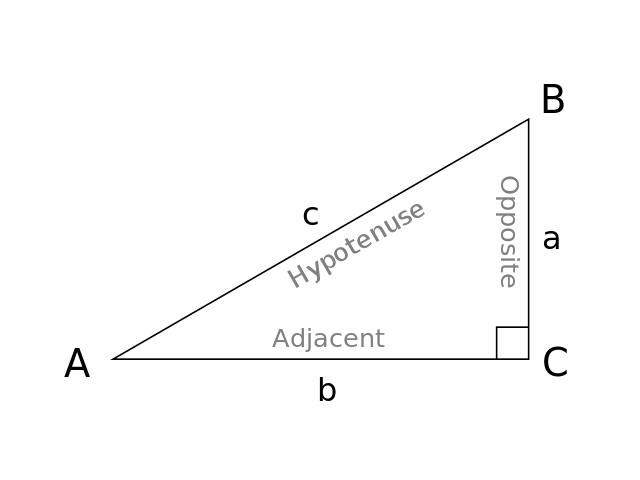
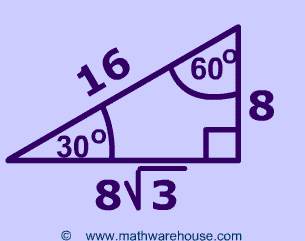
And because this is a triangle, and we were told that the shortest side is 8, the hypotenuse must be 16 and the missing side must be $8 * √3$, or $8√3$ Our final answer is 8√3 The TakeAways Remembering the rules for triangles will help you to shortcut your way through a variety of math problemsA triangle is a right triangle where the three interior angles measure 30° 30 °, 60° 60 °, and 90° 90 ° Right triangles with interior angles are known as special right triangles Special triangles in geometry because of the powerful relationships that unfold when studying their angles and sidesYou can use the Pythagorean Theorem to find the length of the hypotenuse of a right triangle if you know the length of the triangle's other two sides, called the legs
How to Solve a Triangle Education is knowing that triangles have three properties laid out in the theorem Wisdom is knowing what to do with that knowledgeRight Triangles, Pythagorean Theorem and , DRAFT 10th 11th grade times Mathematics 70% average accuracy 2 years ago peggyrenier 0 Save Edit I have been given the short leg in this triangle How do I find the length of the hypotenuse?Pythagorean Inequalities Theorem Definition Suppose that there is a Triangle ABC in which Sides A & B are the legs, and Side C is the longest side If C^2>A^2B^2, then the triangle is an obtuse triangle, and if C^2
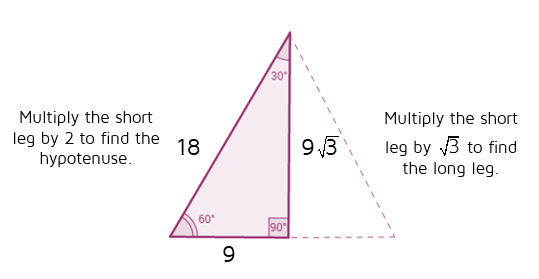
Two triangles sharing a long leg form an equilateral triangle;Note A triangle is a special right triangle with some very special characteristics If you have a triangle, you can find a missing side length without using the Pythagorean theorem!Example of 30 – 60 90 rule Example 1 Find the missing side of the given triangle As it is a right triangle in which the hypotenuse is the double of one of the sides of the triangle Thus, it is called a triangle where smaller angle will be 30 The longer side is always opposite to 60° and the missing side measures 3√3 units in



The Easy Guide To The 30 60 90 Triangle




Relationships Of Sides In 30 60 90 Right Triangles Ck 12 Foundation
Concurrency of Medians of a Triangle 30°60°90° Triangle Theorem 45°45°90° Triangle Theorem Trigonometric Ratios Inverse Trigonometric Ratios Area of a Triangle Polygons and Circles Polygon Exterior Angle Sum Theorem m 1 = m 2 Definition of congruent anglesUse the Pythagorean theorem to discover patterns in 30°60°90° and 45°45°90° triangles If you're seeing this message, it means we're having trouble Triangle Theorem, Properties & Formula / in Feeds / by Munene david This lesson will explore a specific kind of right triangle, the right triangle, including the relationships that exist between the sides and angles in them Special Triangles




30 60 90 Triangle Sides Examples Angles Full Lesson




30 60 90 Triangle Theorem Ratio Formula Video
The hypothenuse of the following 30 60 90 triangle measures {eq}8 {/eq} cm Use this to determine the lengths of the other sides Angle Bisector Theorem Definition and ExampleWhat I want to do in this video is discuss a special class of triangles called triangles and I think you know why they're called this the measures of its angles are 30 degrees 60 degrees and 90 degrees and what we're going to prove in this video this tends to be a very useful result at least for a lot of what you see in a geometry class and then later on in trigonometry class is the The triangle having the three angles as 30^0, 60^0 and 90^0 is the Scalene Right Triangle Related Posts Acute Angled Triangle (Definition,




30 60 90 Right Triangle Side Ratios Expii



Special Right Triangles
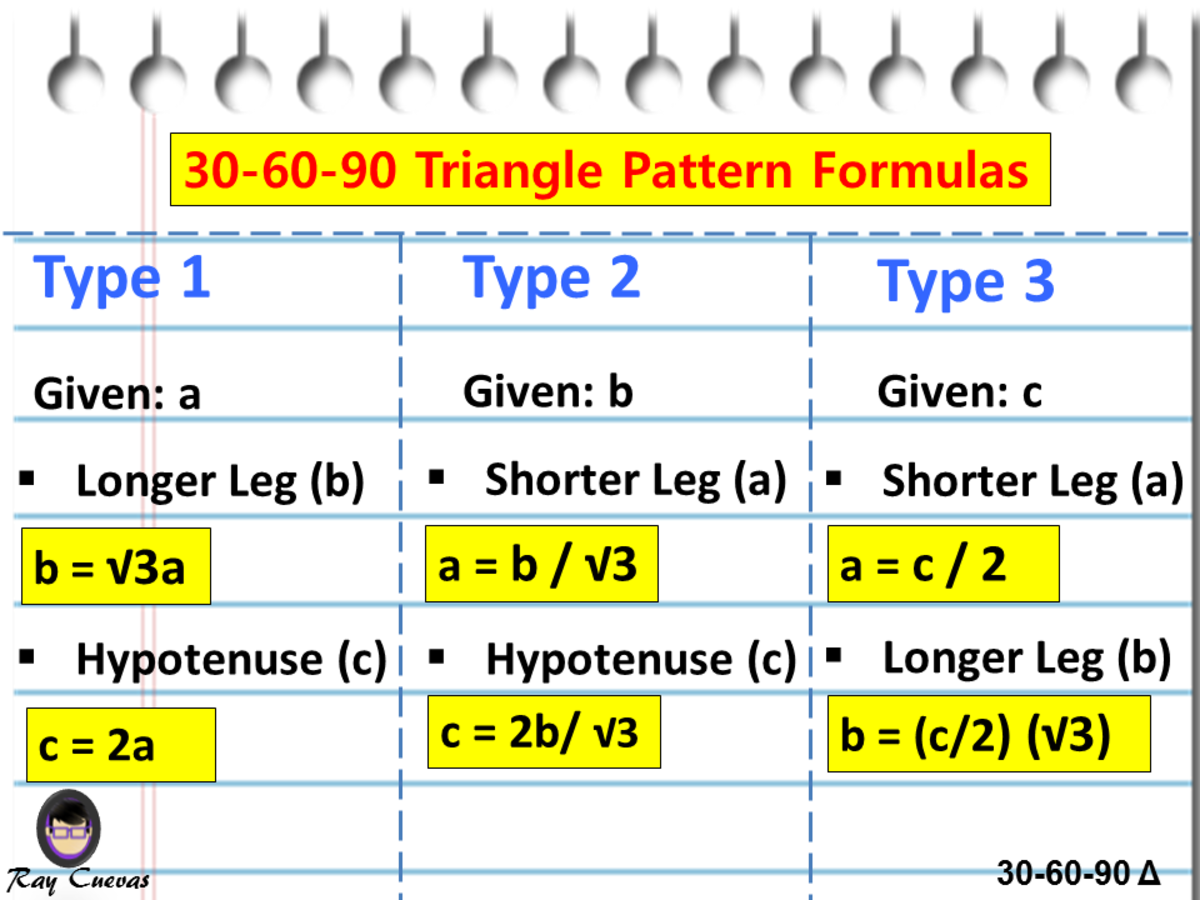
30 60 90 triangle sides If we know the shorter leg length a, we can find out that b = a√3 c = 2a If the longer leg length b is the one parameter given, then a = b√3/3 c = 2b√3/3 For hypotenuse c known, the legs formulas look as follows a = c/2Start studying Chapter 8 Pythagorean Theorem, Triangles, Triangles, Trigonometry Learn vocabulary, terms, and more with flashcards, games, and other study toolsThe triangle is called a special right triangle as the angles of this triangle are in a unique ratio of 123 Here, a right triangle means being any triangle that contains a 90° angle A triangle is a special right triangle that always has angles of measure 30°, 60°, and 90°



5 5 Special Triangles




30 60 90 Triangle Theorem Proof Don T Memorise Youtube
30 60 90 Triangle Theorem Examples The right triangle is a special case triangle, with angles measuring 30, 60, and 90 degrees This free geometry lesson introduces the subject and provides examples for calculating the lengths of sides of a triangle30 60 90 triangle theorem definition If so, then your textbook will supply the formulae How to find the sides of the given triangle definition, 2 examples, and their solutions Formula A triangle is a triangle whose interior angles are 30º, 60º, and 90º The triangle is a special right triangle, and knowing it can save you a lot of time on standardized tests like the SAT and ACT Because its angles and side ratios are consistent, test makers love to incorporate this triangle into problems, especially on the nocalculator portion of



30 60 90 Triangle Formulas Rules And Sides Science Trends




30 60 90 Triangle Theorem Ratio Formula Video
There are three types of special right triangles, triangles, triangles, and Pythagorean triple triangles How do I find the length of a triangle? A 30, 60, 90 triangle is a right triangle It's one of the most common triangles to use to learn about the Pythagorean theorem This is a triangle with one side length given Let's find the length of the other two sides, a and b Since the side you are given, 8, is across from the 30 degree angle, it




30 60 90 Triangle Explanation Examples




How To Work With 30 60 90 Degree Triangles Education Is Around
In any triangle, the side opposite the smallest angle is always the shortest, while the side opposite the largest angle is always the longest You can see hoTHE 30°60°90° TRIANGLE THERE ARE TWO special triangles in trigonometry One is the 30°60°90° triangle The other is the isosceles right triangle They are special because, with simple geometry, we can know the ratios of their sides Theorem In a 30°60°90° triangle the sides are in the ratio 1 2 We will prove that belowA triangle is a special right triangle with some very special characteristics If you have a degree triangle, you can find a missing side length without using the Pythagorean theorem!



Special Right Triangles Formulas 30 60 90 And 45 45 90 Special Right Triangles Examples Pictures And Practice Problems



Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math
30 60 90 triangle rules and properties The most important rule to remember is that this special right triangle has one right angle and its sides are in an easytoremember consistent relationship with one another the ratio is a a√3 2aone right angle and its sides are in an easytoremember consistent relationship with one another theThis video discusses about special triangles in geometry and trigonometry This video has a clear and simple explanation on how to get the measures of the paSolving special right triangles means finding the missing lengths of the sides Instead of using the Pythagorean Theorem, we can use the special right triangle ratios to perform calculations Let's work out a couple of examples Example 1 The longer side of a 30°;



The Easy Guide To The 30 60 90 Triangle



3
Other interesting properties of triangles are All triangles are similar;Definition and properties of triangles Try this In the figure below, drag the orange dots on each vertex to reshape the triangle Note how the angles remain the same, and it maintains the same proportions between its sidesDefinition and properties of triangles Try this In the figure below, drag the orange dots on each vertex to reshape the triangle Note how the angles remain the same, and it maintains the same proportions between its sides



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




Special Right Triangle Wikipedia
Triangle in trigonometry In the study of trigonometry, the triangle is considered a special triangleKnowing the ratio of the sides of a triangle allows us to find the exact values of the three trigonometric functions sine, cosine, and tangent for the angle 45° For example, sin(45°), read as the sine of 45 degrees, is the ratio of the side opposite theAnswer choices Multiply 4 by 2 Multiply 4 by √3 Multiply 4 byTriangles are special right triangles with unique properties, rules, and ratios Use the triangle theorem and formula to find the hypotenuse



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




30 60 90 Triangle Theorem Ratio Formula Video
30 60 90 Triangle Theorem Definition Triangle Midsegment Theorem The midsegment of a triangle is Triangle Inequality Theorem The sum of any two sides of a triangle is greater than the triangle's third side Pythagorean Theorem of the len Pythagorean Inequalities Theorem Triangle Theorem Triangle Theorem If all three sides of one triangle are congruent to theA triangle is one of the few special right triangles with angles and side ratios that are consistent and predictable Specifically, every triangle has a 30º angle, a 60º angle, and a 90º angle Since these angles stay the same, the ratio between the length of the sides also remains the sameCheck out this tutorial to learn about triangles!



30 60 90 Triangle Examples Math Geometry Showme




Special Right Triangles Review Article Khan Academy
Triangle Theorem, Properties & Formula / in Feeds / by Davie This lesson will explore a specific kind of right triangle, the right triangle, including the relationships that exist between the sides and angles in them Special TrianglesAlthough all right triangles have special features – trigonometric functions and the Pythagorean theoremThe most frequently studied right triangles, the special right triangles, are the 30, 60, 90 Triangles followed by the 45, 45, 90 trianglesCheck out this tutorial to learn about triangles!



30 60 90 Triangle Rules



The Easy Guide To The 30 60 90 Triangle
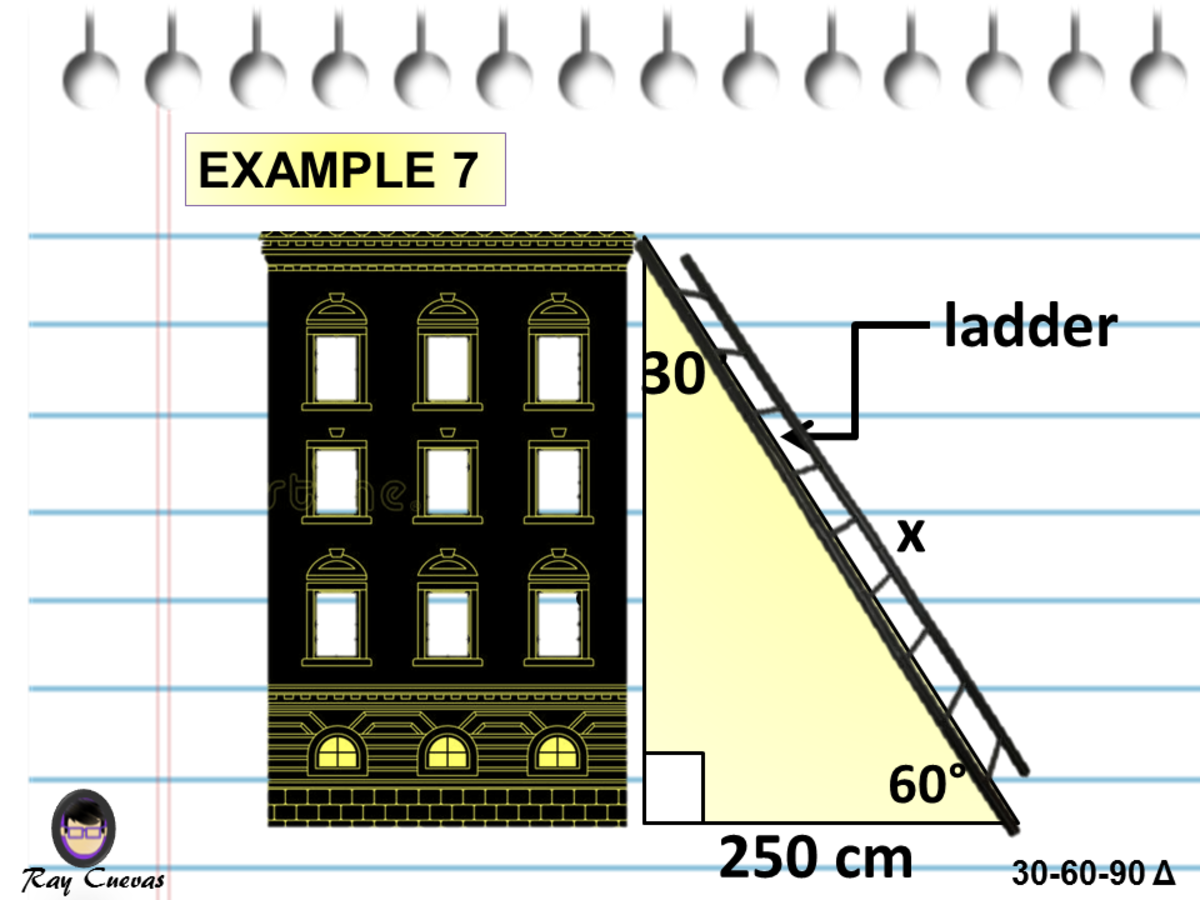
If you add 30 to 90 you get 1 180 minus 1 leaves you with 60 degrees for that third angle Now that we know it's a 30 60 90 triangle, we can apply our 30 60 90 rules to finding the length of our ramp Our ramp is across from the 9030 60 90 Triangle Theorem Proof The triangle is a special right triangle, and knowing it can save you a lot of time on standardized tests like the SAT and ACT Because its angles and side ratios are consistent, test makers love to incorporate this triangle into problems, especially on the nocalculator portion of the SAT




30 60 90 Triangle Definition Math Open Reference



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




30 60 90 Triangle Definition Theorem Formula Examples
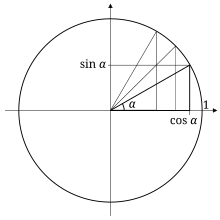



Special Right Triangle Wikipedia
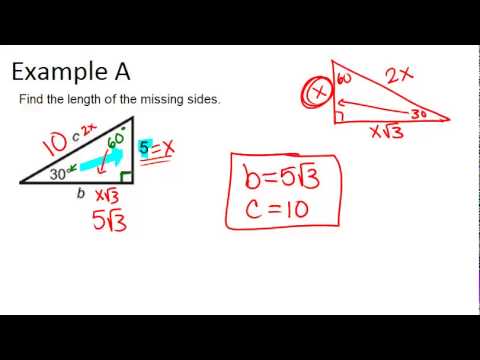



30 60 90 Right Triangles Examples Geometry Concepts Youtube



Why In A 30 60 90 Triangle Is The The Side Opposite 60 Degrees X Sqrt 3 Quora
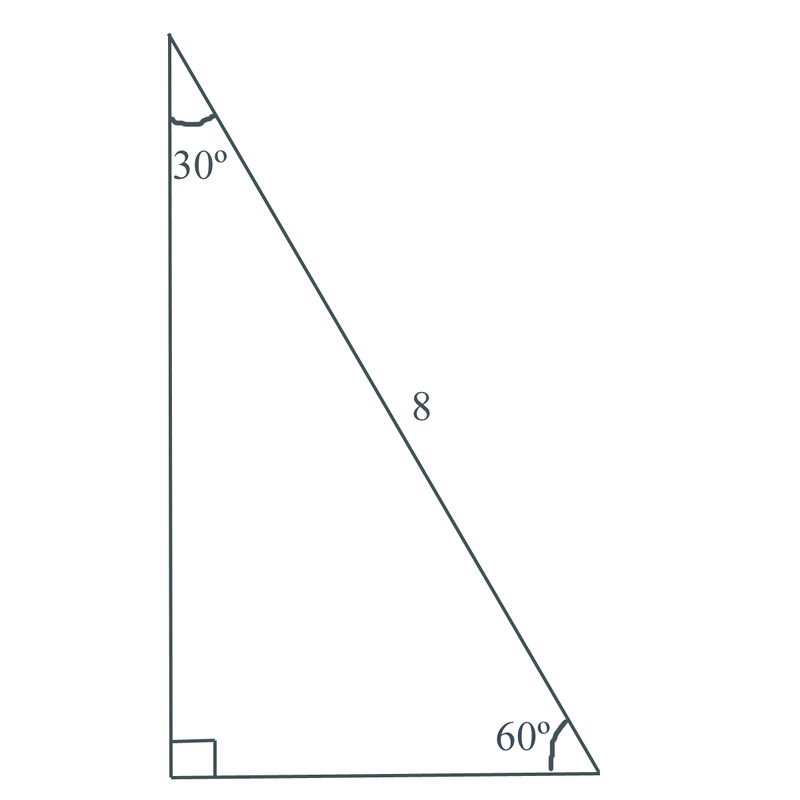



Relationships Of Sides In 30 60 90 Right Triangles Ck 12 Foundation




How To Use The Special Right Triangle 30 60 90 Studypug



Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math




The Complete Guide To The 30 60 90 Triangle
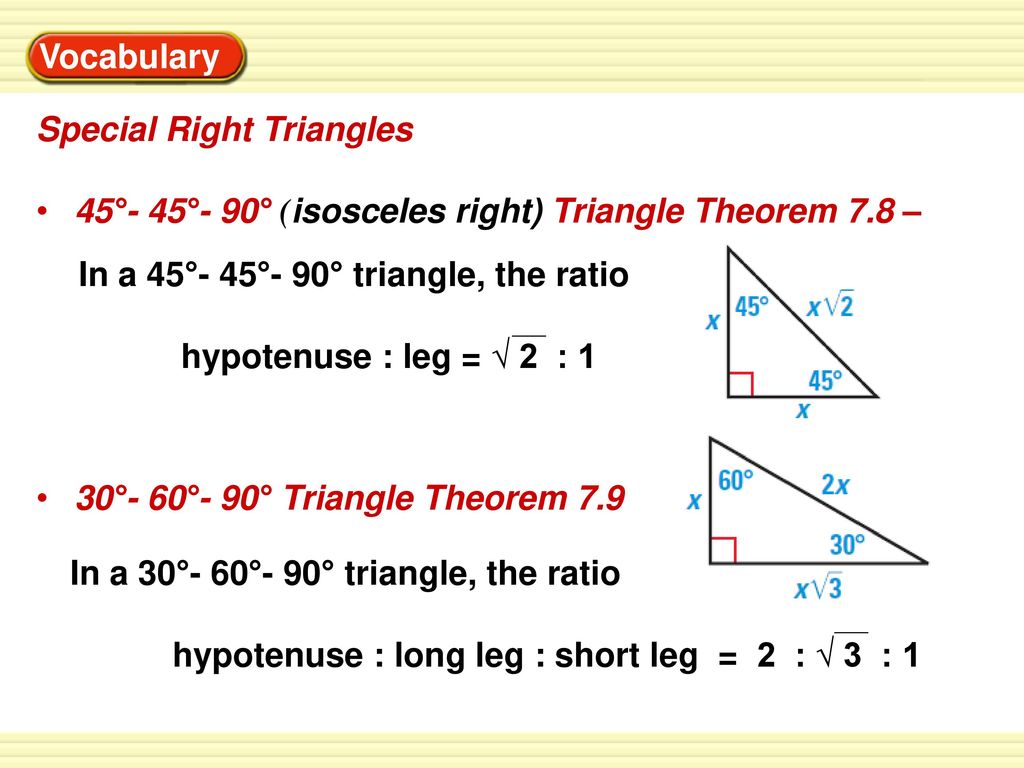



Simplify Answer Answer 12 Answer Ppt Download




30 60 90 Triangle Rules Sides Ratio Of A 30 60 90 Triangle Video Lesson Transcript Study Com




45 45 90 Triangle Theorem Rules Formula Video Lesson Transcript Study Com




30 60 90 Triangles Hd Youtube




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




The 30 60 90 Triangle Topics In Trigonometry



Mrwadeturner 30 60 90 Triangle 6th



The Easy Guide To The 30 60 90 Triangle




1 2 Special Right Triangles Mathematics Libretexts



What Is A 30 60 90 Degree Triangle Virtual Nerd




30 60 90 Triangle Theorem Ratio Formula Video



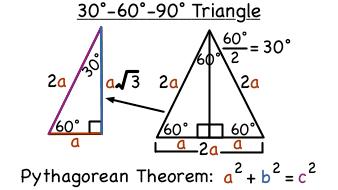
30 60 90 Triangles P4 Kate S Math Lessons




Applying The 30 60 90 Triangle To Height Youtube




30 60 90 Triangle Calculator Formula Rules




30 60 90 Triangles




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com
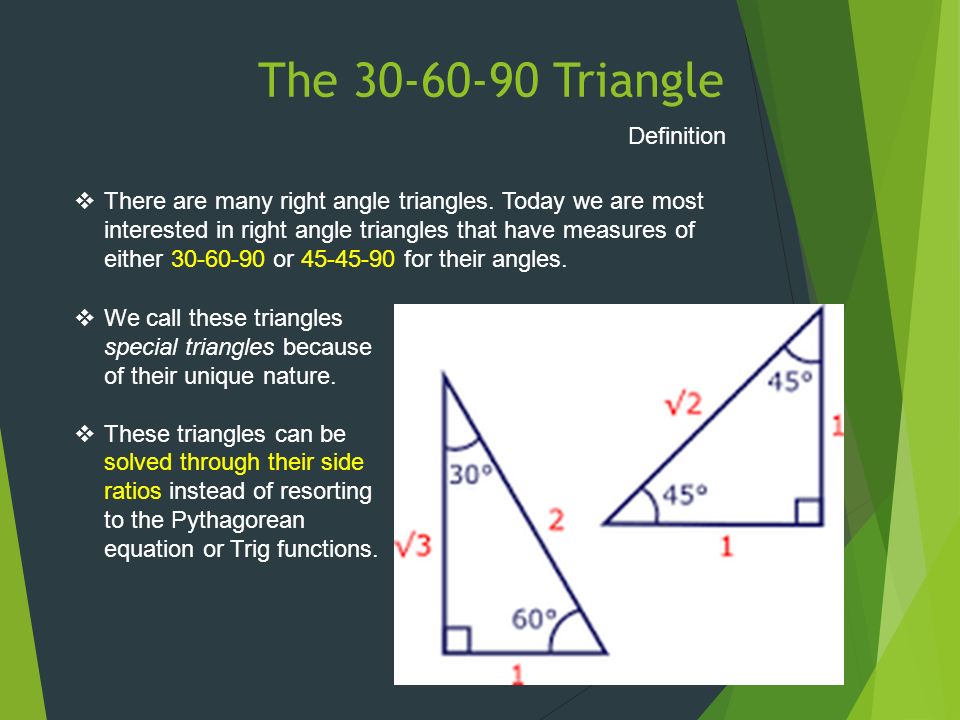



Special Right Triangles Definition And Use The Triangle Definition There Are Many Right Angle Triangles Today We Are Most Interested In Right Ppt Download
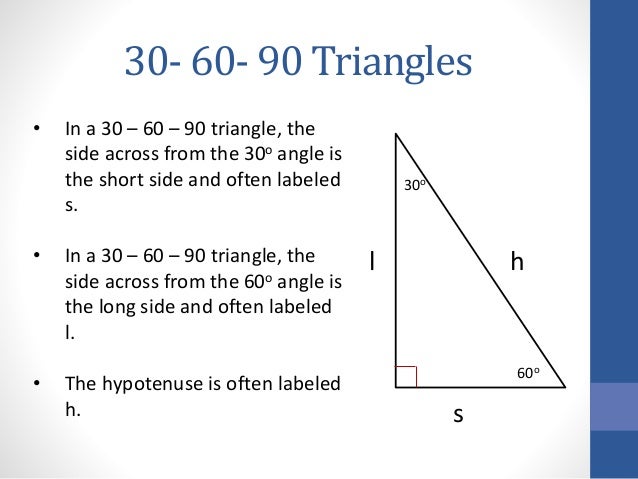



30 60 90 Triangles




30 60 90 Triangle Theorem Ratio Formula Video



How To Work With 30 60 90 Degree Triangles Education Is Around
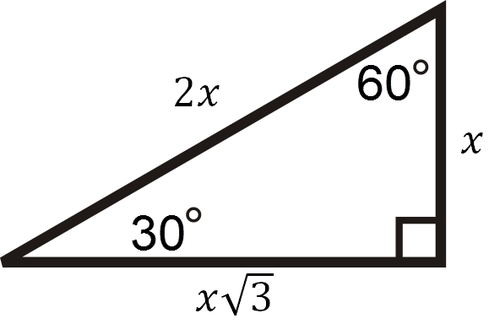



Special Right Triangles Read Geometry Ck 12 Foundation
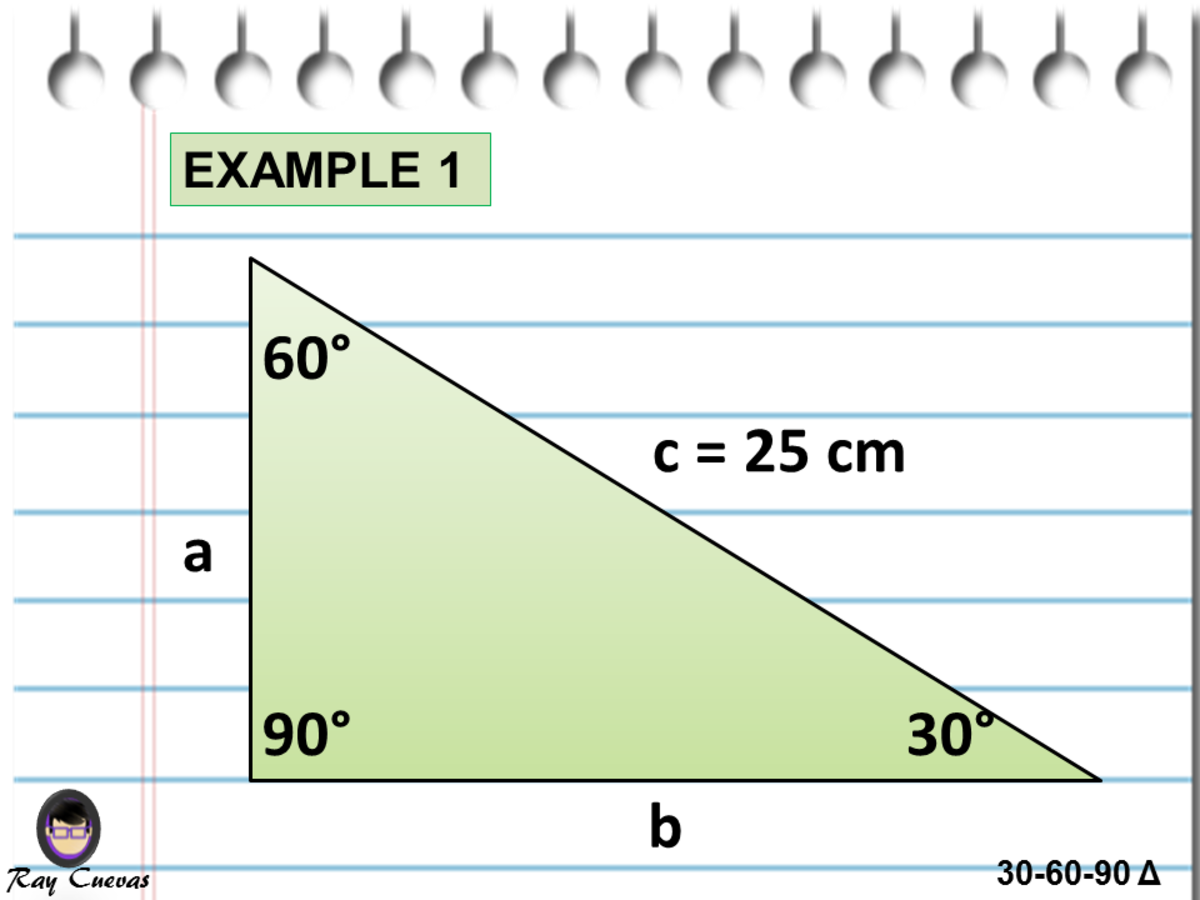



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




30 60 90 Right Triangles Ck 12 Foundation




Special Right Triangle Wikipedia




30 60 90 Triangle Definition Theorem Formula Examples



1
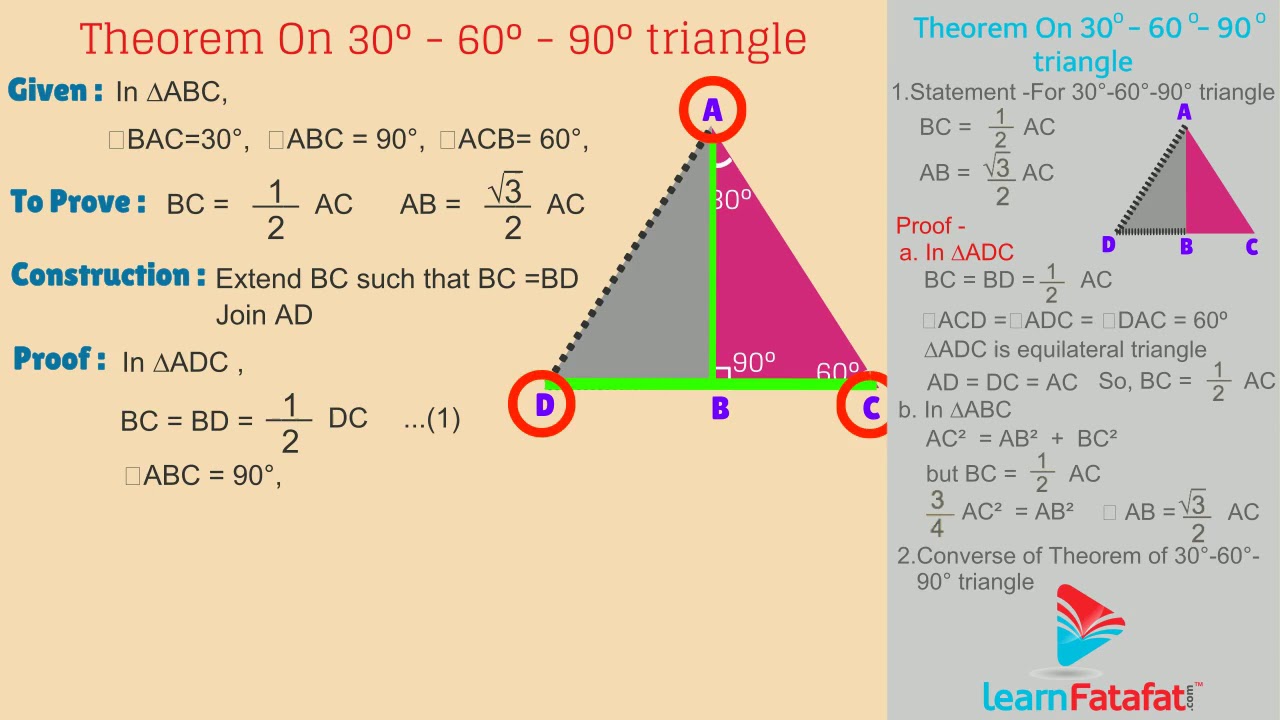



Pythagoras Theorem On 30 60 90 Triangle Youtube
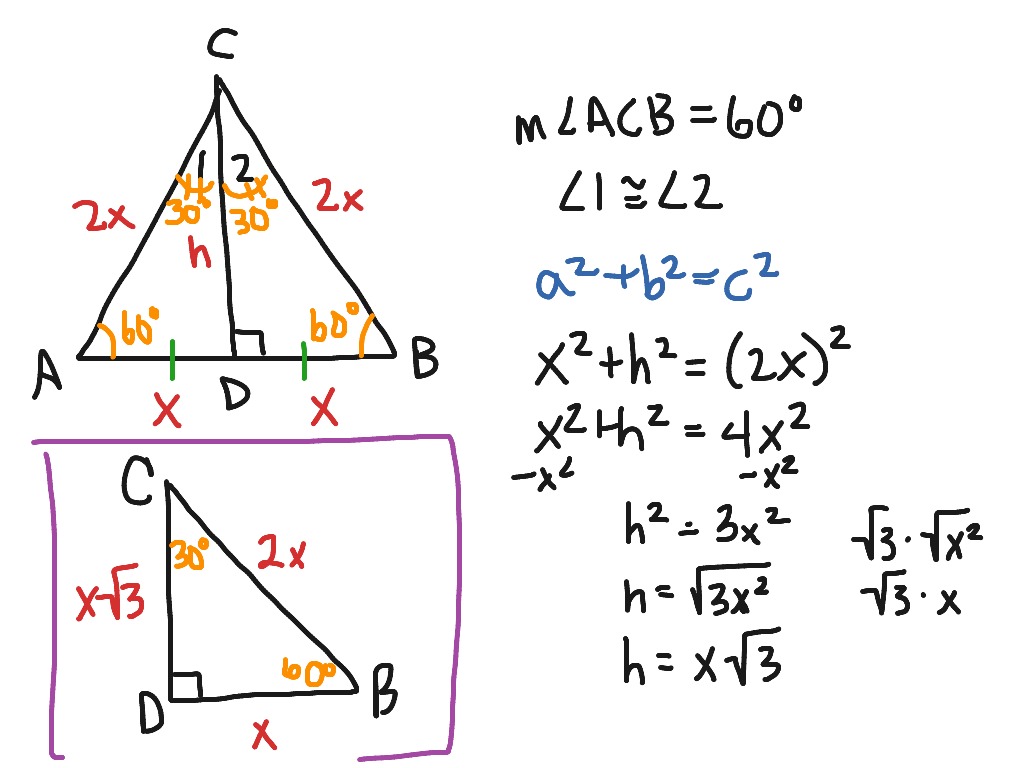



30 60 90 Triangle Math Right Triangles Showme




5 8b 30 60 90 Special Right Triangles Youtube




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
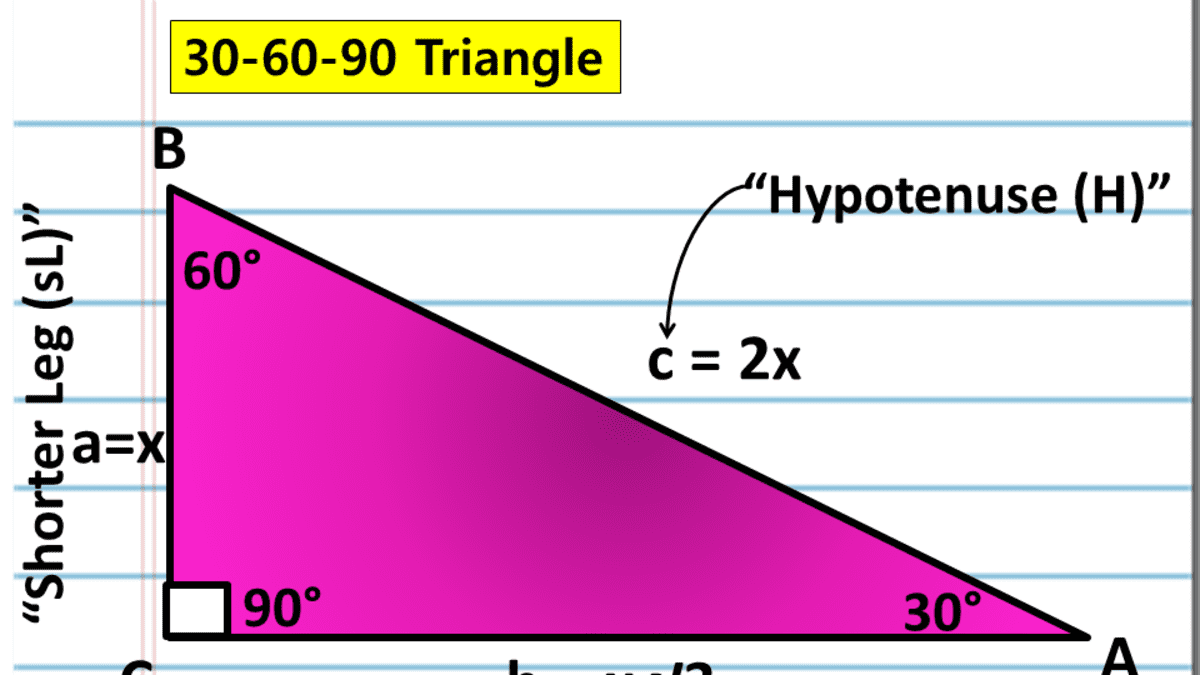



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




The Complete Guide To The 30 60 90 Triangle



1




Special Right Triangles Video Lessons Examples And Solutions




30 60 90 Right Triangles Ck 12 Foundation




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com




Special Right Triangles Fully Explained W 19 Examples




30 60 90 Triangles Special Right Triangle Trigonometry Youtube




30 60 90 Triangle Theorem Ratio Formula Video
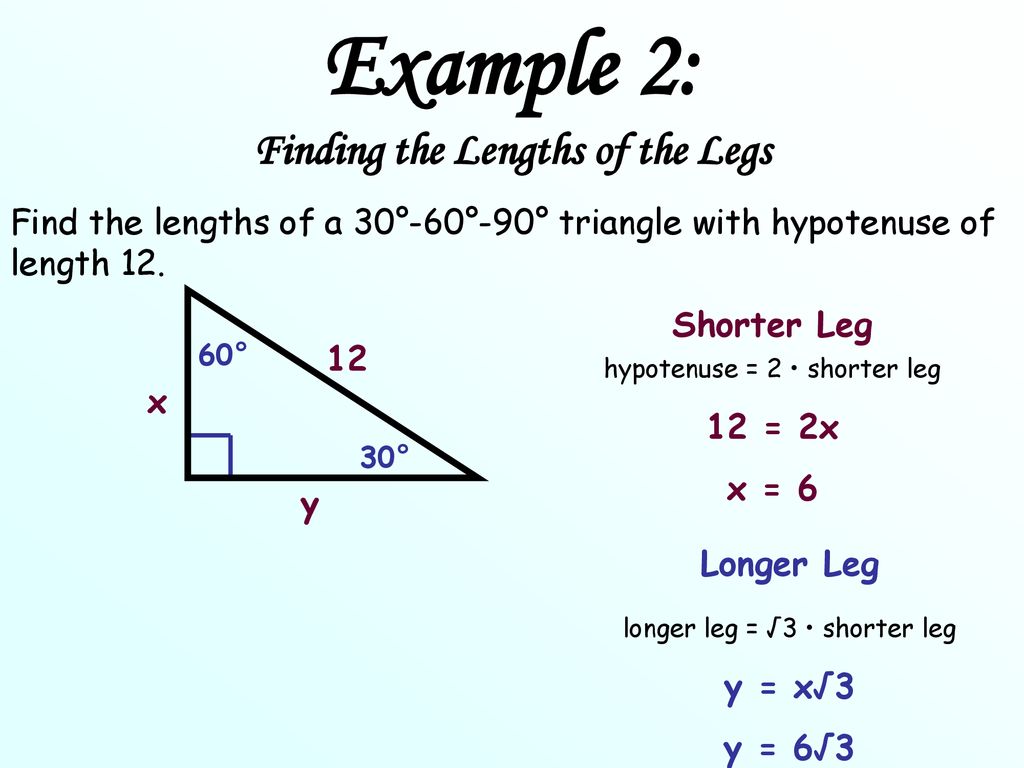



Objective To Use The Properties Of 30 60 90 Triangle Ppt Download




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Triangle Definition Theorem Formula Examples




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com




30 60 90 Triangle Calculator Formula Rules




A Quick Guide To The 30 60 90 Degree Triangle Dummies




Learn About The 30 60 90 Triangle Caddell Prep Online



30 60 90 Triangle Definition Theorem Formula Examples
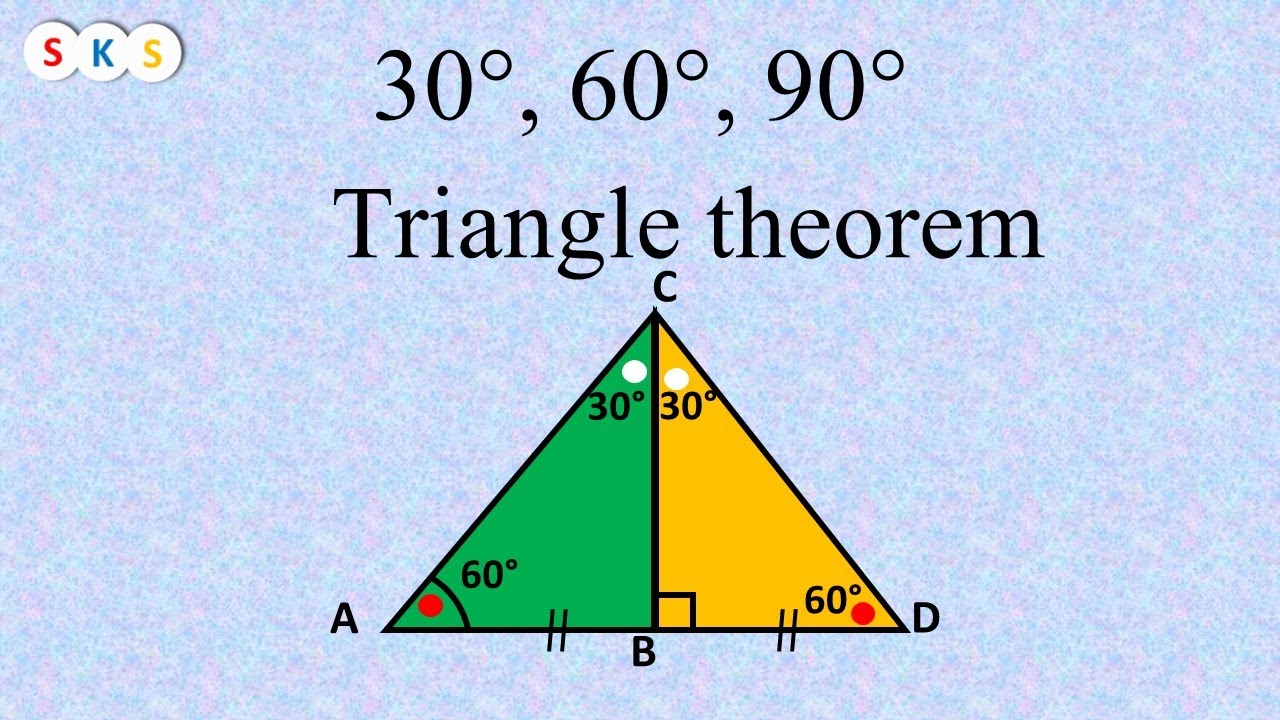



30 60 90 Triangle Theorem Proof I Triangle I Theorem Of 30 60 90 Triangle Proof Youtube
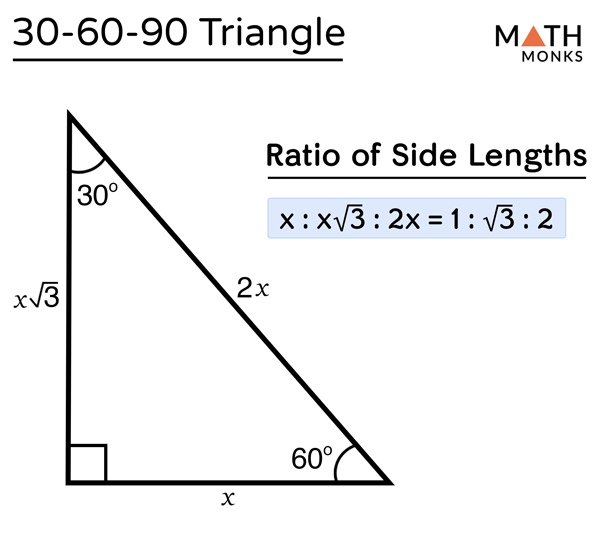



30 60 90 Triangle Definition Formulas Examples
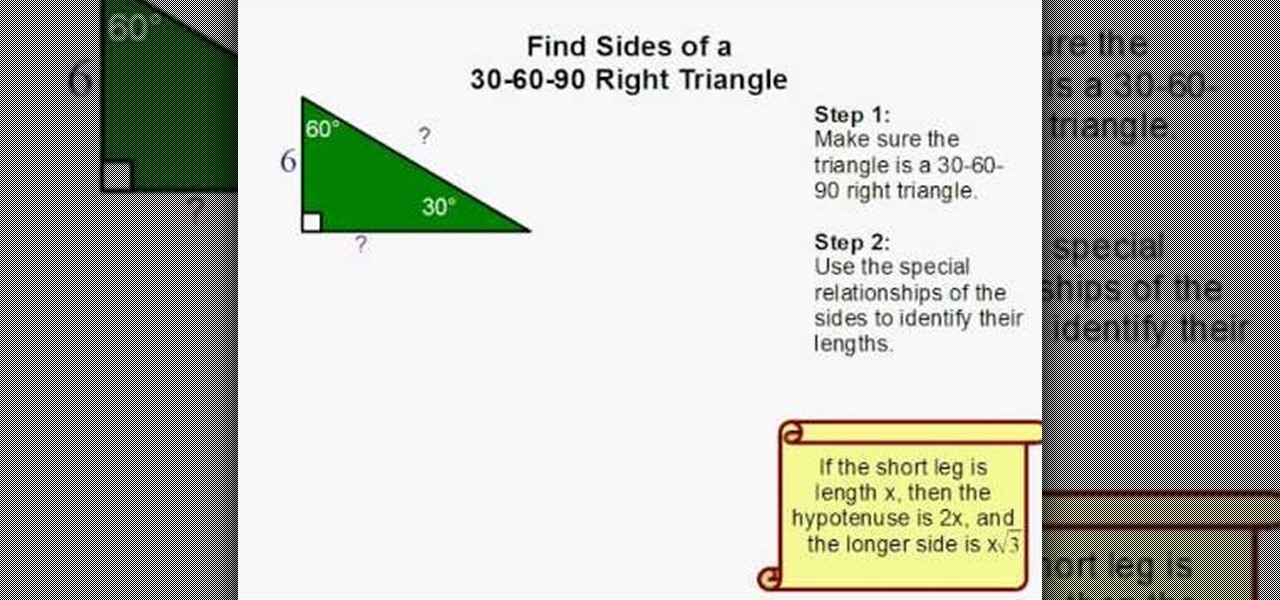



How To Find The Sides Of A 30 60 90 Right Triangle Math Wonderhowto




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com




30 60 90 Right Triangles Lesson Geometry Concepts Youtube




30 60 90 Triangle Example Problem Video Khan Academy




30 60 90 Right Triangles Solutions Examples Videos




30 60 90 Triangle Theorem Ratio Formula Video
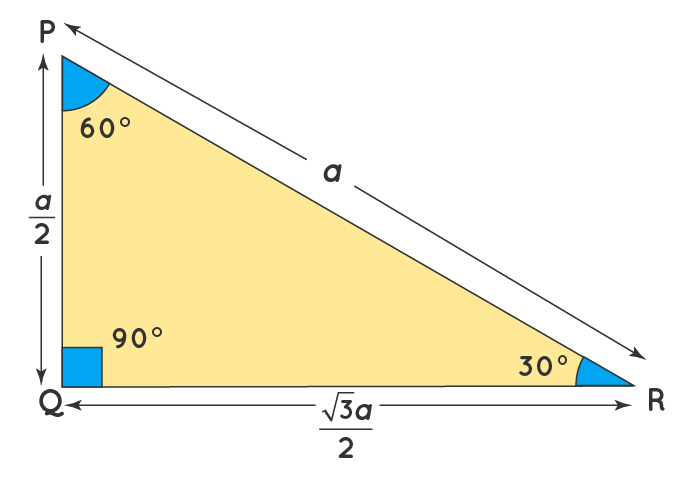



30 60 90 Triangle Definition Theorem Formula Examples




30 60 90 Right Triangles Ck 12 Foundation




Special Right Triangles Interactive Notebook Page Math Methods Teaching Geometry Teaching Math




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation



45 45 90 And 30 60 90 Triangles Zona Land Education




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Right Triangles Ck 12 Foundation




30 60 90 Triangles




A Quick Guide To The 30 60 90 Degree Triangle Dummies
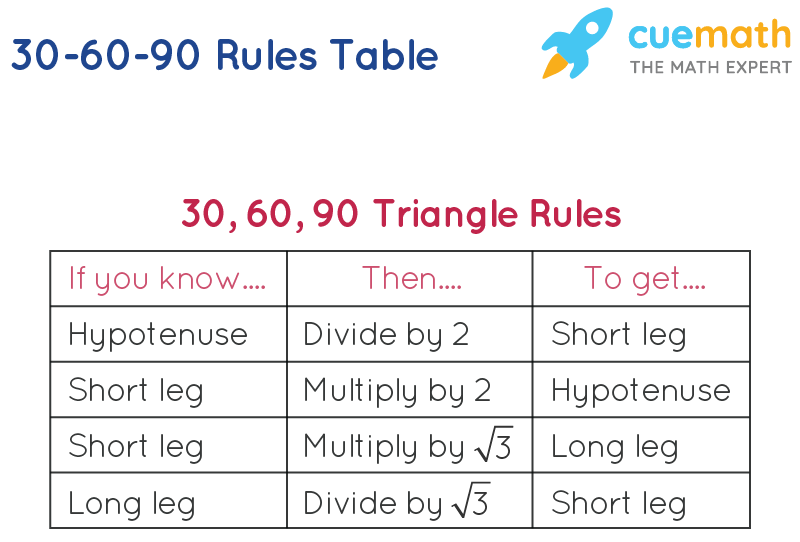



30 60 90 Formula Learn Formula For Calculating The 30 60 90 Measures



1




30 60 90 Triangle Explanation Examples



The 30 60 90 Triangle Topics In Trigonometry



30 60 90 Triangle Definition Formulas Examples



0 件のコメント:
コメントを投稿