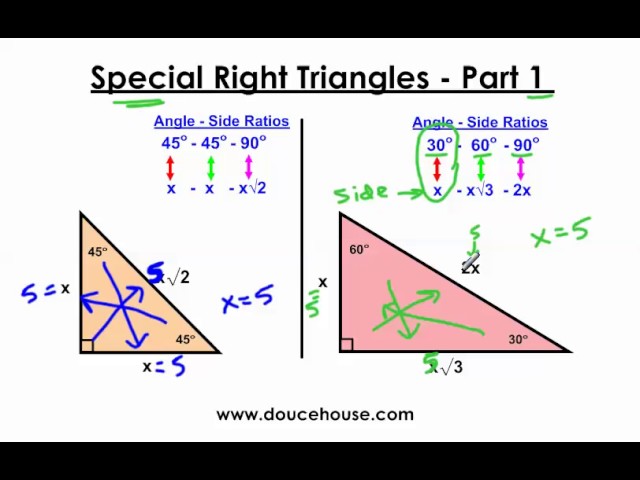
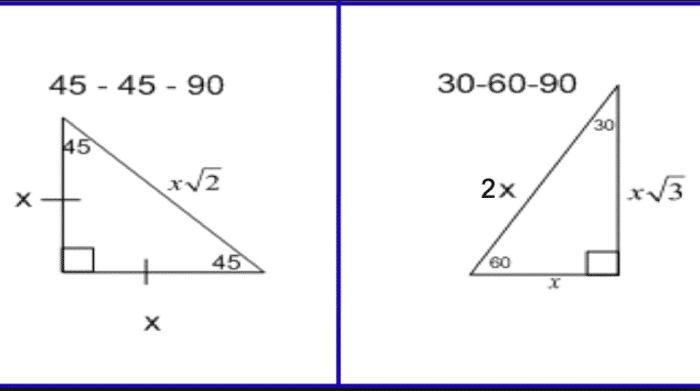
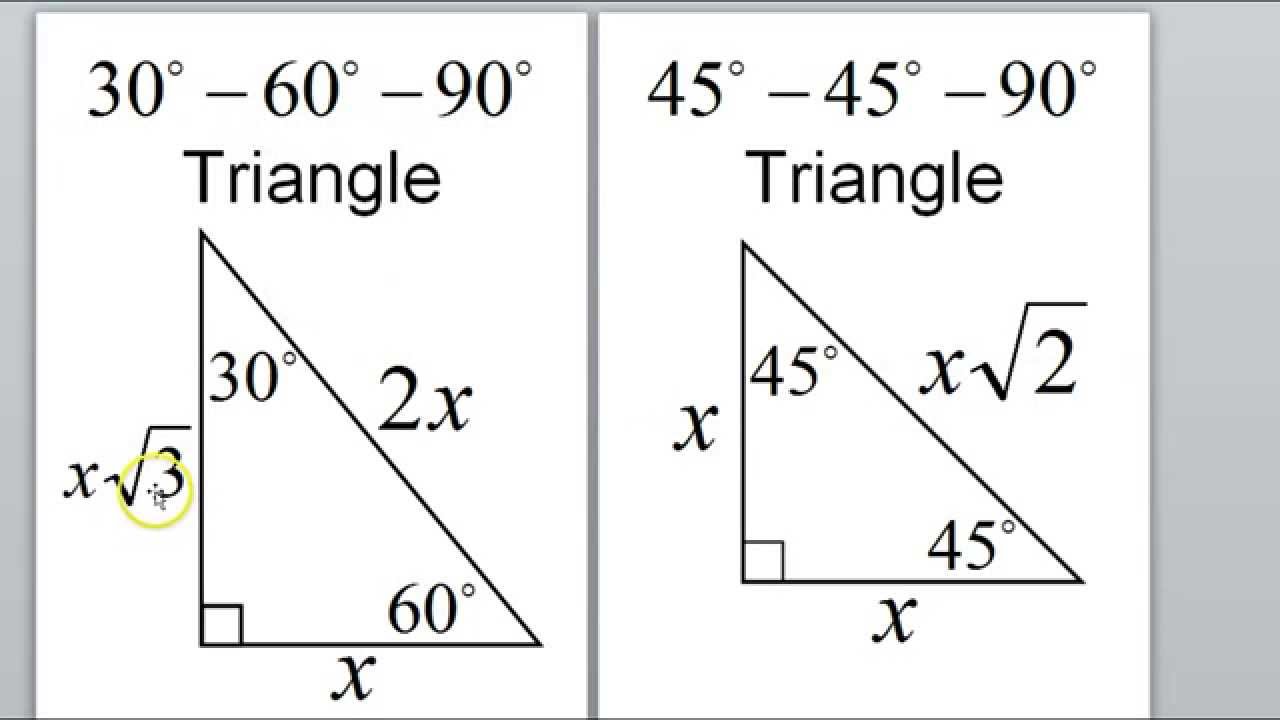
The 45 45 90 triangleA triangle is a right triangle where the three interior angles measure 30 °, 60 °, and 90 ° Right triangles with interior angles are known as special right triangles Special triangles in geometry because of the powerful relationships thatWhat is special about 30 60 90 triangles is that the sides of the 30 60 90 triangle always have the same ratio Therefore, if we are given one side we are able to easily find the other sides using the ratio of 12square root of three This special type of right triangle is similar to the 45 45 90 triangle 90 and 30, 60, 90 triangles
Special Right Triangles Fully Explained W 19 Examples
Special right triangles 30 60 90 and 45 45 90
Special right triangles 30 60 90 and 45 45 90-These activity cards include special right triangles There are 18 cards for and 9 cards that cover They can be printed on cardstock for durability Place page 1 and 3, then 2 and 4 together and print 2 sided for correct flashcardsA 30 60 90 triangle is a special right triangle a right triangle being any triangle that contains a 90 degree angle that always has degree angles of 30 degrees 60 degrees and 90 degrees In a 45 45 90 triangle the hypotenuse is 2 times as long as each leg




Special Right Triangle Wikipedia
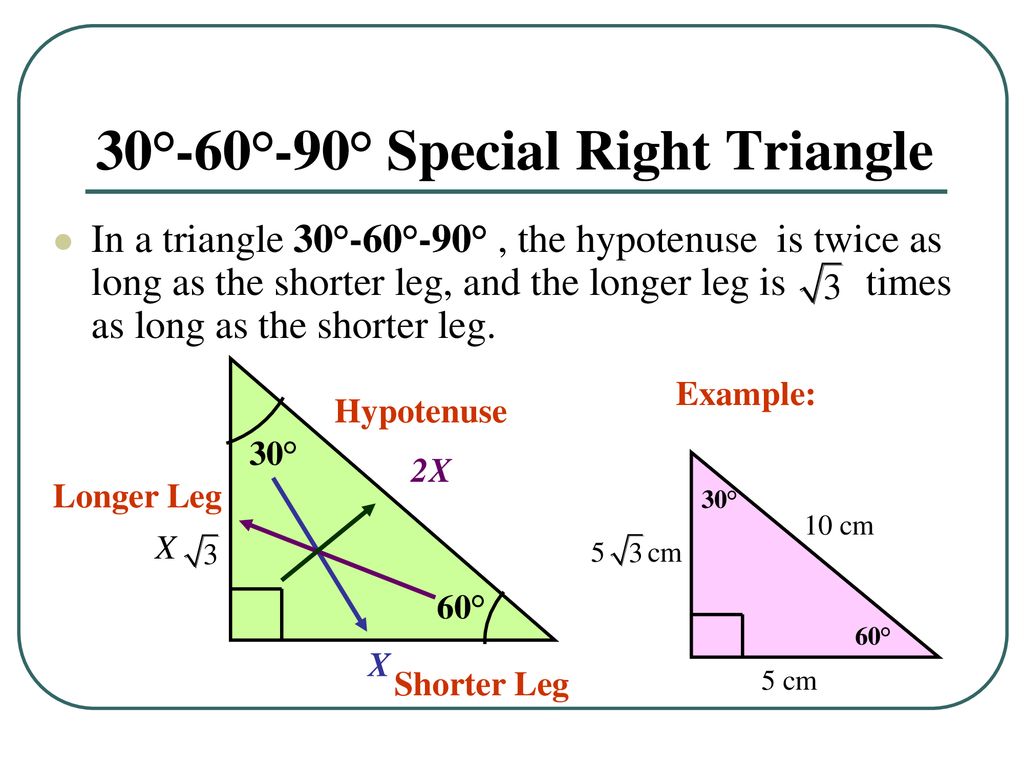
Special Shortcuts for and Triangles Triangle If you know the length of the leg, multiply that by 2 to find the length of the hypotenuse Triangle If you know the length of the hypotenuse and you want the length of the leg, divide the length of the hypotenuse by 2 Triangle When working with a triangle, you will have three different lengths Short leg Long leg Hypotenuse Triangle If you know the length of the short leg 133 Special Right Triangles, p709 45°45°90° and 30°60°90° This is a 30°60°90° triangle Since the length of the shorter leg is 5 cm, then the length of the hypotenuse is 5 multiply by 2, which gives 10 cm , andScroll down the page if you need more examples and explanations on how to derive and use the trig ratios of special angles Trigonometric Function Values Of Special Angles How to derive the trigonometric function values of 30, 45 and 60 degrees and their corresponding radian measure Cofunction identities are also discussed sin θ = cos(90° θ) cos θ = sin(90° θ) Show Video
Math 1312 Section 55 Special Right Triangles Note 9 hours ago Mathuhedu Visit Site Math 1312 Section 55 Special Right Triangles Note Triangles in this section are always right triangles!Special Right Triangles A special right triangle is one which has sides or angles for which simple formulas exist making calculations easy Of all these special right triangles, the two encountered most often are the 30 60 90 and the 45 45 90 trianglesMath 1312 Section 55 Special Right Triangles Note Triangles in this section are always right triangles!
Done Discovery EXPAND Prior to completing the construction and discovery for Triangle Construction and Discovery, you may need to review how to construct triangles with students This lesson provides scaffolded notes and websites which can be used as review tools Also, a quick review using this applet may help to remindQ Find x the length of the hypotenuse of the triangle Q Find a the length of the hypotenuse Q If the leg of a triangle is 7 cm long, then its hypotenuse is _____ cm Q Find the value of y Q Find the value of y Q Find the value of y Q Find a the length of a leg of the triangleThe toughest thing for many students is to tell the and triangles apart based on their side lengths So, in this video I introduce you to both the fractions and nonfractions versions of these "special" triangles, and I show you tricks to keep the two straight (TIP 90% of the time, if there's a "3" under the square root it's a 3060, and if there's a "2" under any root it's a 4545)



1 30 60 90 Triangle 45 45 90 Triangle Problem 1 Problem 2 Problem 4 Problem 5 Standard End Show Presentation Created By Simon Perez All Rights Ppt Download



Special Angle Values 30 60 90 And 45 45 90 Triangles Purplemath
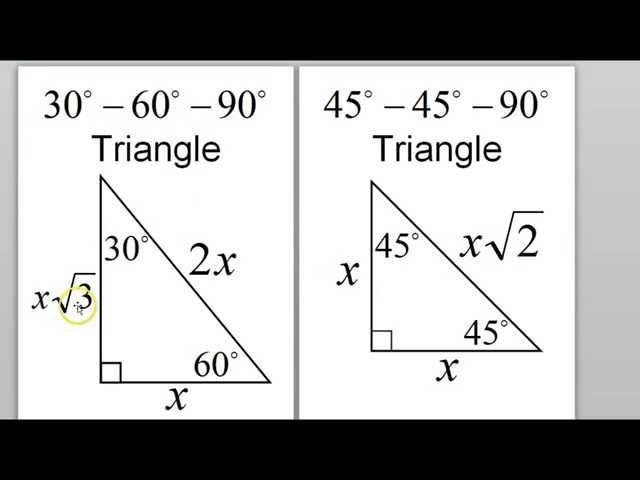
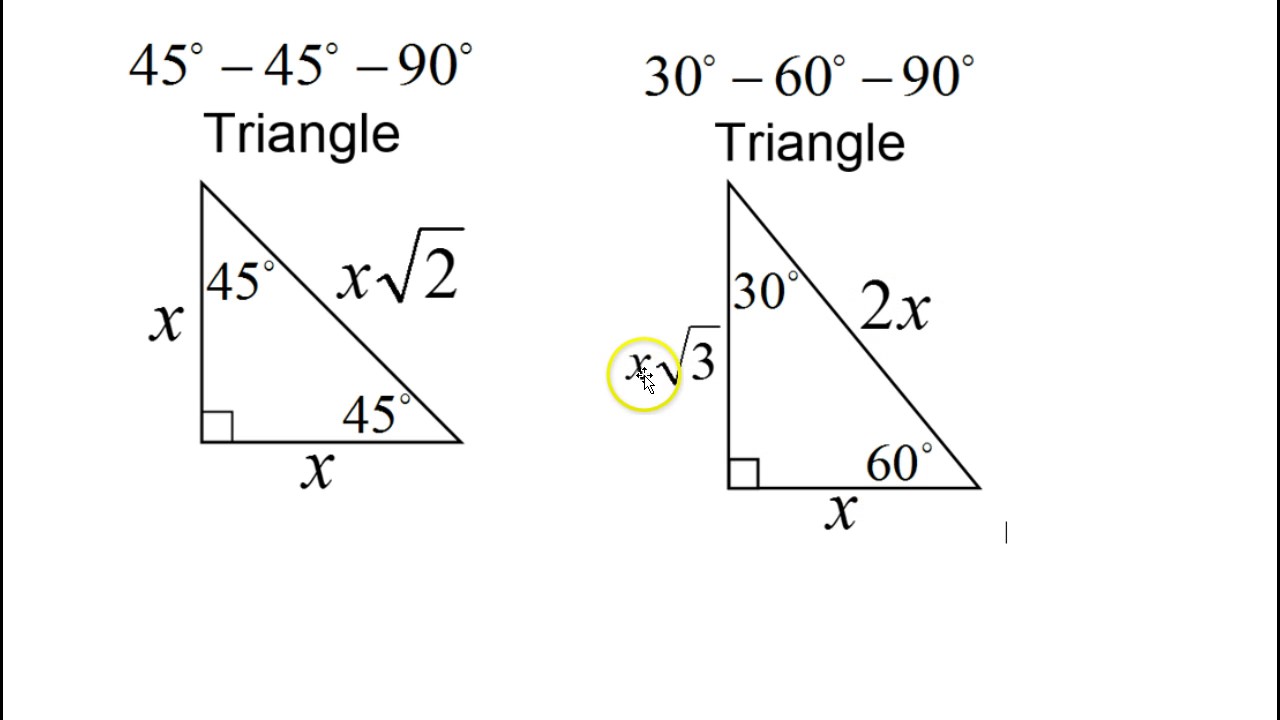
Students will be able to understand the relationships between the side lengths in and triangles, find missing sides and perimeters in and triangles without using trigonometryI introduce and work through 6 examples of problems involving 30 60 90 triangles and 45 45 90 triangles All work is done in exact form and not rounded offTriangles Theorem 1 In a triangle whose angles measure 45 0, 45 0, and 90 , the hypotenuse has a length 0 equal to the product of 2 and the length of either leg The ratio of the sides of a triangle are x x x 2




Mrs Newell S Math Better Questions Special Right Triangles




Special Right Triangles 30 60 90 And 45 45 90 Triangles Matter Of Math
Find out what are the sides, hypotenuse, area and perimeter of your shape and learn about 45 45 90 triangle formula, ratio and rules If you want to know more about another popular right triangles, check out this 30 60 90 triangle tool and the calculator for special right trianglesStudents also learn that in a 30°60°90° triangle, the length of the long leg is equal to root 3 times the length of the short leg, and the length of the hypotenuse is equal to 2 times the length of the short leg Students are then asked to find the lengths of missing sides of 45°45°90° and 30°60°90° triangles using these formulasLearn how to find the missing side in a and special right triangle using the proportion method We go through 2 examples in this video mat




45 45 90 And 30 60 90 Special Right Triangles Practice Hw By Eric Douce




30 60 90 Triangle Sides Examples Angles Full Lesson
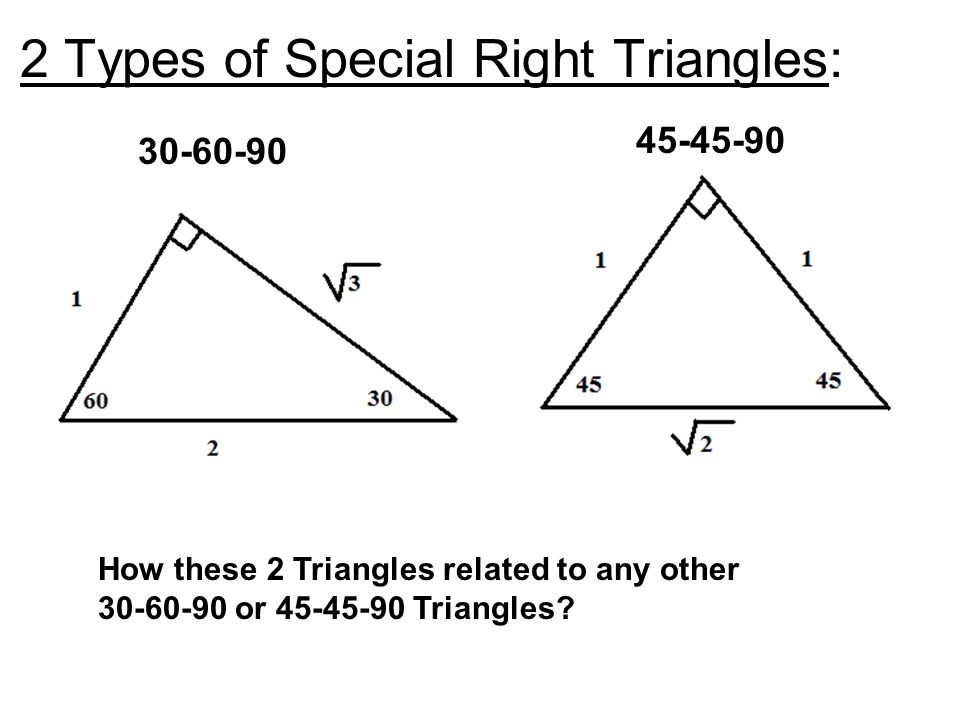
The most frequently studied right triangles the special right triangles are the 30 60 90 triangles followed by the 45 45 90 triangles 2 19 by user linda gregory i use this activity to have my students discover the relationships between the sides on 45 45 90 and 30 60 90 trianglesWhat is a 30°60°90° Triangle?Properties of triangles To identify special right triangle, check



Special Right Triangle Activity Cards 30 60 90 And 45 45 90 By Sarah Branam
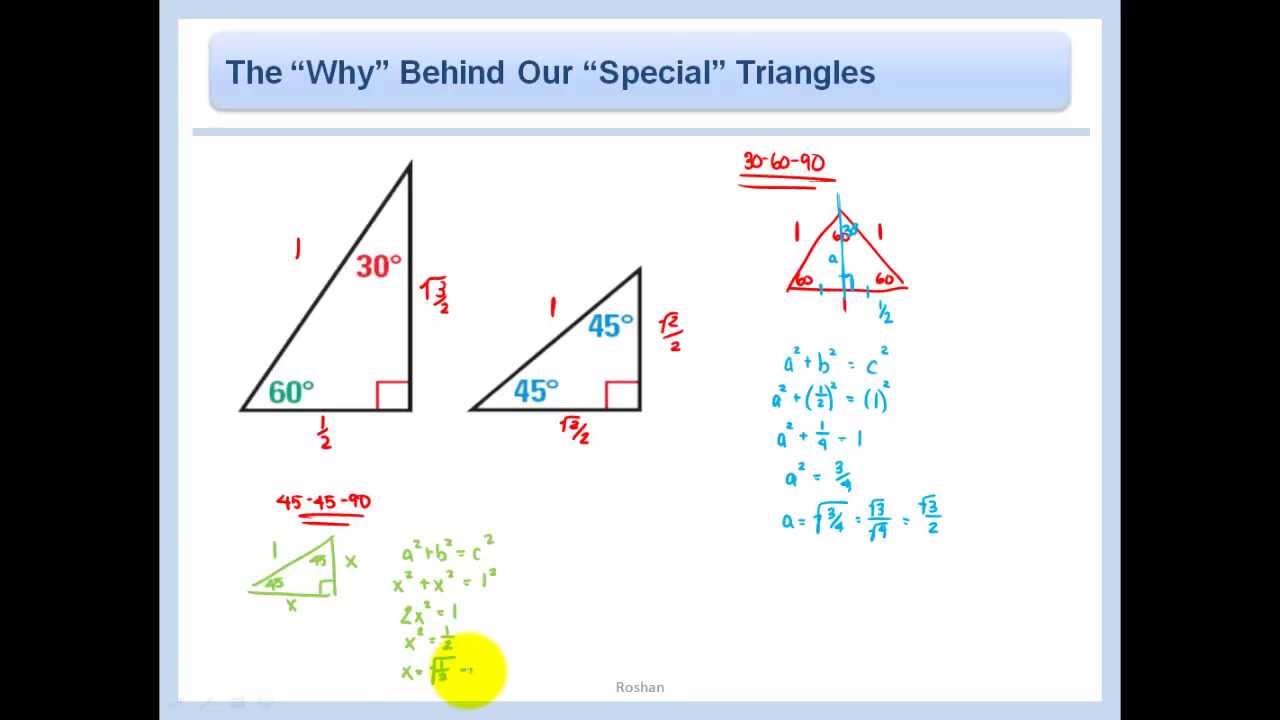



Trigonometry The Why Behind Our Special Triangles 30 60 90 And 45 45 90 Youtube
This is a fun Escape Room activity over solving problems using Special Right Triangles ( and ) There are 15 questions hung around the room (lift the flap style) Working in pairs, the students answer each question The correct answer yields a clue to a 4digit code number The two special right triangles are right triangles with interior angles measuring 30 60 90 and 45 45 90 What is the 45 45 90 triangle rule?Learn shortcut ratios for the side lengths of two common right triangles 45°45°90° and 30°60°90° triangles The ratios come straight from the Pythagorean theorem




Special Right Triangle Wikipedia




Special Right Triangles Review Article Khan Academy
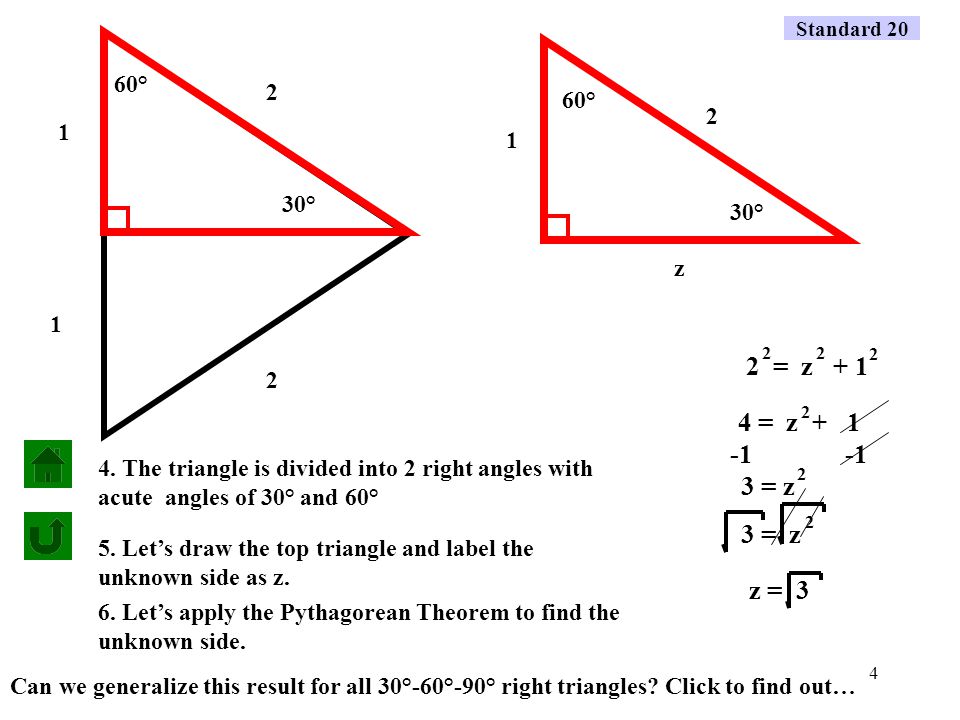
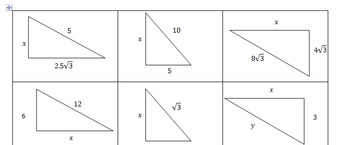
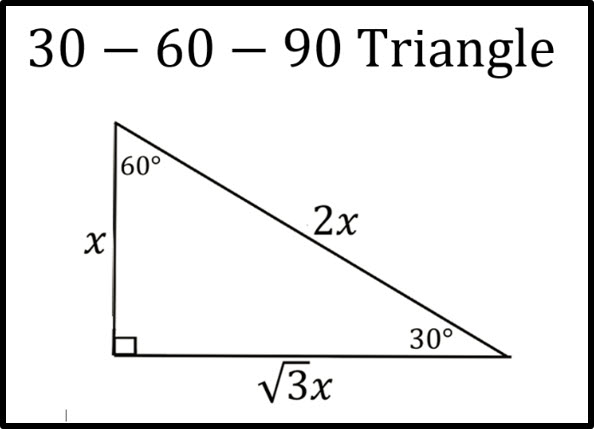
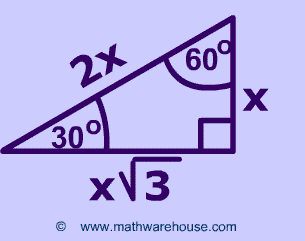
300 Find the length of the diagonal Location of the short side of a triangle What is opposite the 30 degree angle? These are the two most common right triangles For degrees, the ratio is 1 1 √ 2 For degrees, the ratio is 1 √ 3 2 Other concepts to remember are that in any triangle a larger angle corresponds to longer sideSpecial Right Triangles long 30 hypotenuse leg 600 short leg 450 hypotenuse leg 450 leg short leg = hypotenuse long leg (short leg) hypotenuse = 2 (short leg) legs are equal hypotenuse = (leg) Use the and triangle relationships to solve for the missing sides



Special Right Triangles Formulas 30 60 90 And 45 45 90 Special Right Triangles Examples Pictures And Practice Problems



Pythagorean Triples Andymath Com
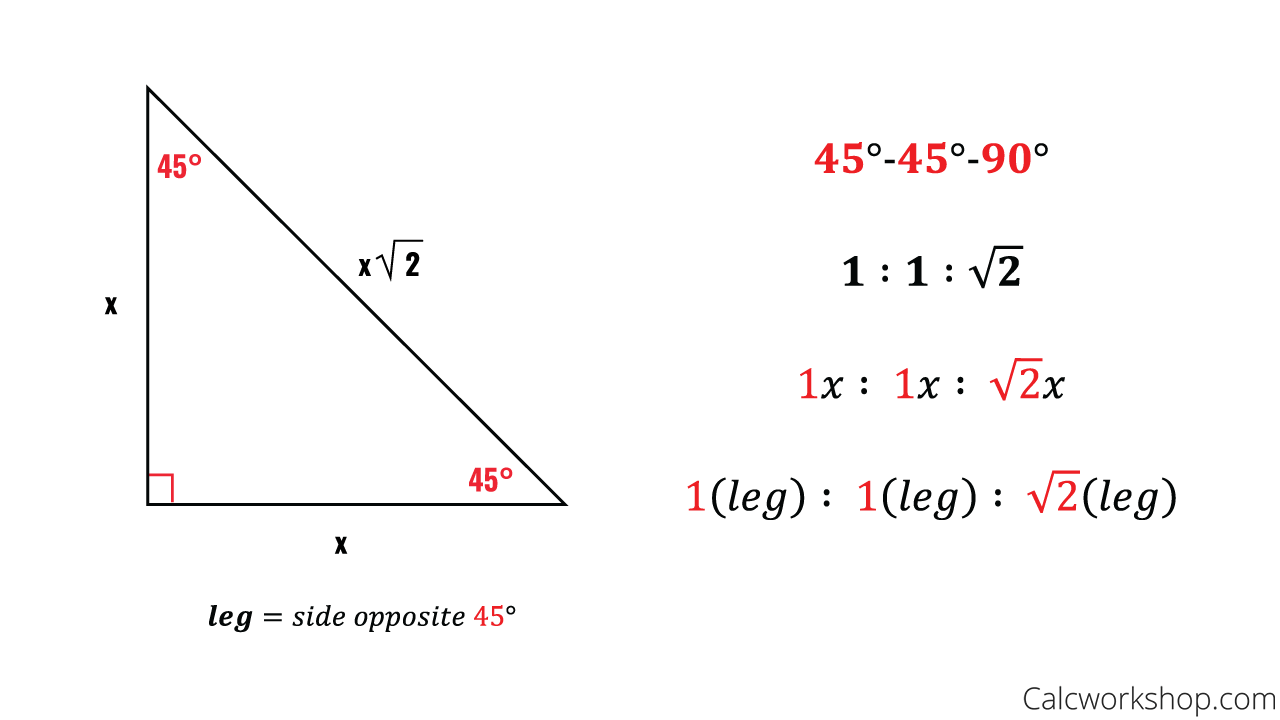
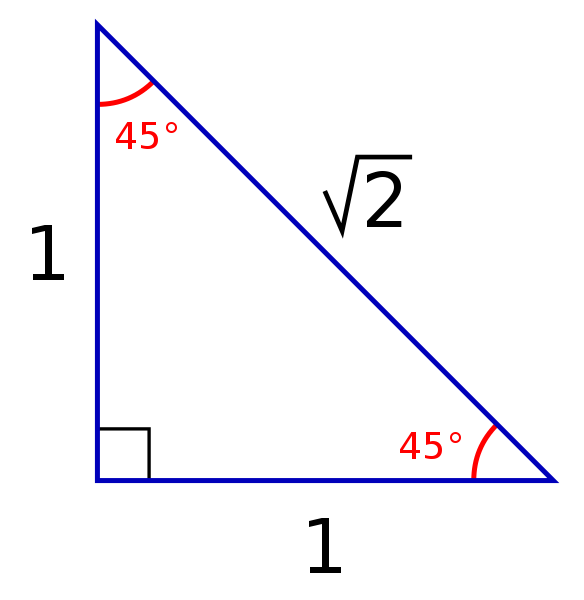
The triangle has three unique properties that make it very special and unlike all the other triangles triangle ratio There are two ratios for triangles The ratio of the sides equals 1 1 2;Special Right Triangles Although all right triangles have special features – trigonometric functions and the Pythagorean theorem The most frequently studied right triangles, the special right triangles, are the 30, 60, 90 Triangles followed by the 45, 45, 90 trianglesThe special right triangle that is formed by drawing the diagonal of a square Another name for the triangle What is an isosceles right triangle?




Special Right Triangle Wikipedia



Buy Triangle Set 10 Inch 30 60 45 90 In Cheap Price On Alibaba Com
Special Right Triangles in Geometry and degree triangles This video discusses two special right triangles, how to derive the formulas to find the lengths of the sides of the triangles by knowing the length of one side, and then does a few examples using themTriangles Theorem 1 In a triangle whose angles measure 45 0, 45 0, and 90 , the hypotenuse has a length 0 equal to the product of 2 and the length of either legSpecial triangles , across from 30 1 across from 60 square root 3 hypotenuse 2 across from the 45s




Special Right Triangles Video Lessons Examples And Solutions




Right Triangles Special Right 45 45 30 60 90 Thanksgiving Riddle Worksheet
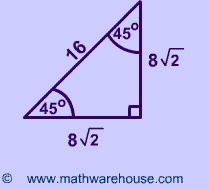
One of these right triangles is named a triangle, where the angles in the triangle are 45 degrees, 45 degrees, and 90 degrees This is an isosceles right triangle The other triangle is named a triangle, where the angles in the triangle are 30 degrees, 60 degrees, and 90 degrees Common examples for the lengths of the sides are shown for each below Thanks to all of you who support me on Patreon You da real mvps!Although all right triangles have special features – trigonometric functions and the Pythagorean theoremThe most frequently studied right triangles, the special right triangles, are the 30, 60, 90 Triangles followed by the 45, 45, 90 triangles




Geometry 8 2b 45 45 90 30 60 90 Triangles Youtube
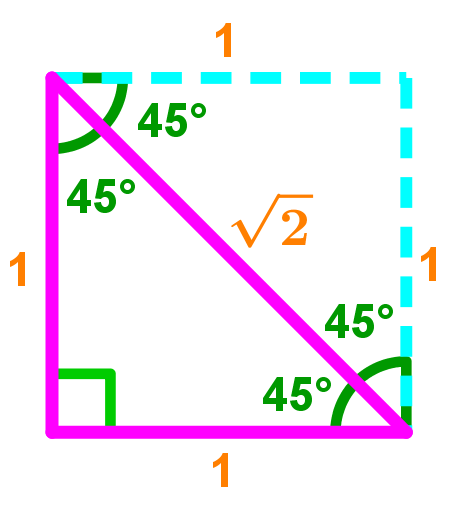



How To Use The Special Right Triangle 45 45 90 Studypug
Learn how to find the missing sides of a Triangle and a using the proportion method, the equation method and the shortcut method in this ma400 Find the hypotenuse of this triangle Special Right Triangles (, ) Created by user Linda Gregory I use this activity to have my students discover the relationships between the sides on and triangles Materials required rulers Activity Download Special_Right_Trianglesdocx Activity Answer Key



Solved Advanced Geemetry Ws 3 Special Right Triangles Chegg Com



2
Special Right Triangles inSpecial Right Triangles and the This resource includes diagrams with side ratios followed by problems for each side of special right triangles Pages 1 and 2 have problems followed by sentence structures to help students connect the ratio between the leg of a triangle with Subjects Math, Geometry, Trigonometry1 If a trig question is asking for the answer to be in "exact value" form, this is likely going to require the use of a special triangle This may be a 45 45 90 triangle of perhaps a 30 60 90 triangle Recall that with special triangle trigonometry, we do not have to round or use decimals due to the unique ratios between the lengths of the sides




Special Right Triangles Exploration 30 60 90 And 45 45 90 Full Package Right Triangle Special Right Triangle Simplifying Radicals




30 60 90 And 45 45 90 Triangles Youtube
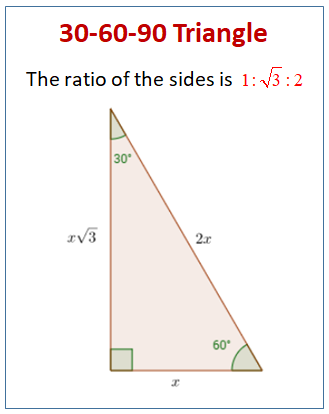
Start studying Special right triangles 45,45,90 60,30,90 Learn vocabulary, terms, and more with flashcards, games, and other study toolsAnother type of special right triangles is the 30°60°90° triangle This is right triangle whose angles are 30°60°90° The lengths of the sides of a 30°60°90° triangle are in the ratio of 1 √3 2 You can also recognize a 30°60°90° triangle A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one another
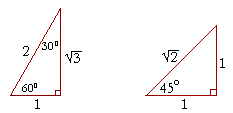



The 30 60 90 Triangle Topics In Trigonometry




Special Right Triangles 30 60 90 And The 45 45 90 Graphic Organizer Worksheet Special Right Triangle Right Triangle Math Lessons
If you want to read more about that special shape, check our calculator dedicated to the 30° 60° 90° triangle Special right triangles 45 45 90 Another famous special right triangle is 45° 45° 90° triangleThe ratio of the angles equals 1 1 2;Special Right Triangles Use the and triangle relationships to solve for the missing sides Use the answers to reveal the name of the team that Abraham M Saperstein established and sent on the road in 1927



1
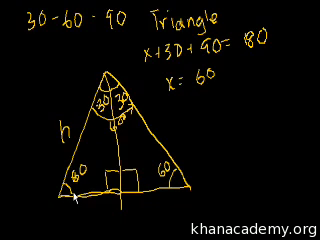



Special Right Triangles Intro Part 2 Video Khan Academy
A http//wwwdoor2mathcom production Dr Pan makes learning math Fun triangleThe hypotenuse is 60 I need to find "x", otherwise known as the legsSpecial triangles – Formula and examples Special triangles are right triangles that have special proportions for their sides The 30°60°90° triangle has the proportions 1√32 The 45°45°90° triangle has the proportions 11√2 All the lengths of these sides can be easily found if we only know the length of one of the sides$1 per month helps!!



Unique Bargains Students 30 60 45 Degree Plastic Triangle Rulers Protractor Drawing Set 2 Pcs Walmart Com



1
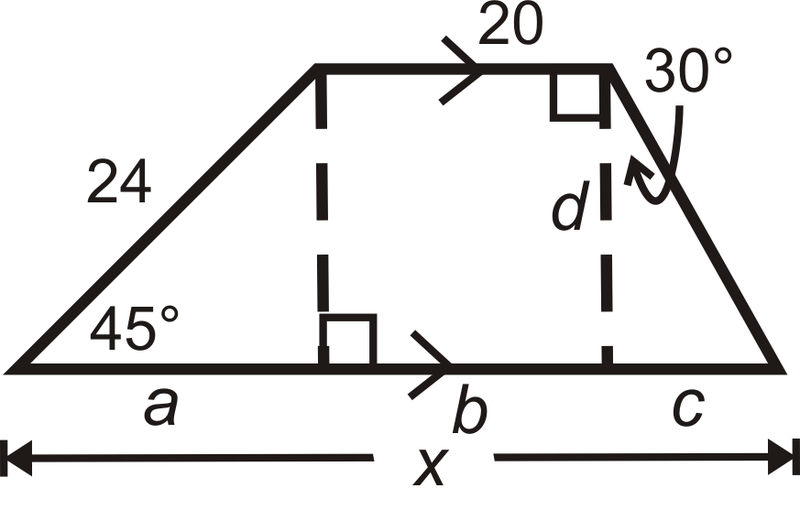
Students are asked to solve advanced problems using the 45°45°90° and 30°60°90° triangle formulas, such as finding the missing parts of a rhombus, a trapezoid, or an equilateral triangle



45 45 90 Triangles Lessons Blendspace



Student Difficulty With Special Right Triangles 45 45 90 And 30 60 90 In Geometry Matheducation




Mrs Newell S Math Better Questions Special Right Triangles




Mathcounts Notes Special Right Triangles 30 60 90 And 45 45 90 Degrees Right Triangles




30 60 90 Right Triangles Ck 12 Foundation




Special Right Triangles 30 60 90 And 45 45 90 Triangles Youtube




Use 45 45 90 Amp 30 60 90 Special Right Triangles To Solve Find The Missing Sir Length Leave You Brainly Com




30 60 90 Right Triangles Solutions Examples Videos



Special




How To Work With 30 60 90 And 45 45 90 Degree Triangles Dummies




Special Right Triangles 30 60 90 45 45 90 Flashcards Quizlet



Special Right Triangles Complete Reference Guide The Education



30 60 90 Right Triangles Ck 12 Foundation




Amazon Com Alvin Clear Acrylic Triangle 2 Piece Set Angle 30 60 And 45 90 Office Products




Special Right Triangles Fully Explained W 19 Examples




Special Right Triangles Fully Explained W 19 Examples
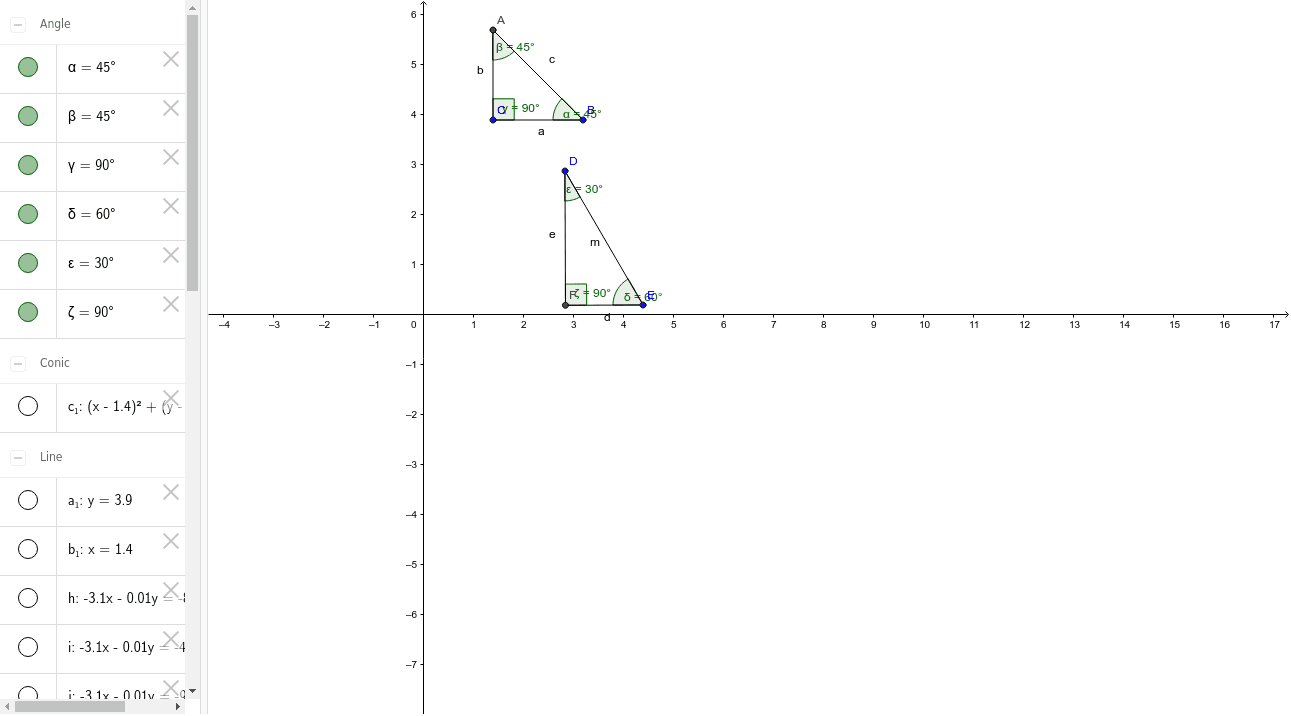



Special Right Triangles 45 45 90 Degree And 30 60 90 Geogebra




The Converse Of The Pythagorean Theorem And Special Triangles Geometry Right Triangles And Trigonometry Mathplanet




Special Right Triangles 30 60 90 And The 45 45 90 Graphic Organizer Worksheet Right Triangle Special Right Triangle Math Review Worksheets



45 45 90 Special Right Triangle Ppt Download



Special Right Triangles 30 60 90 Worksheet Jobs Ecityworks



Day 16 Test C 9 To 12 Special Right Triangles 30 60 90 45 45 90 Youtube




Special Right Triangles 30 60 90 45 45 90 Flashcards Quizlet



45 45 90 Special Right Triangle Calculator Inch Calculator



30 60 90 Triangle Formulas Rules And Sides Science Trends




Special Right Triangles Practice Bundle 45 45 90 And 30 60 90 Tpt



30 60 90 Special Right Triangles Videos Worksheets Examples Solutions




Extra Practice 45 45 9030 60 90 Right Triangles 1xnza92 Pdf Geometry Name Id 1 U00a9h G2n0c1c6j Hkwubthan Xszoqfgtkwzaqrfex Glzluc T H Zaqlzl Course Hero




30 60 90 Right Triangles Ck 12 Foundation
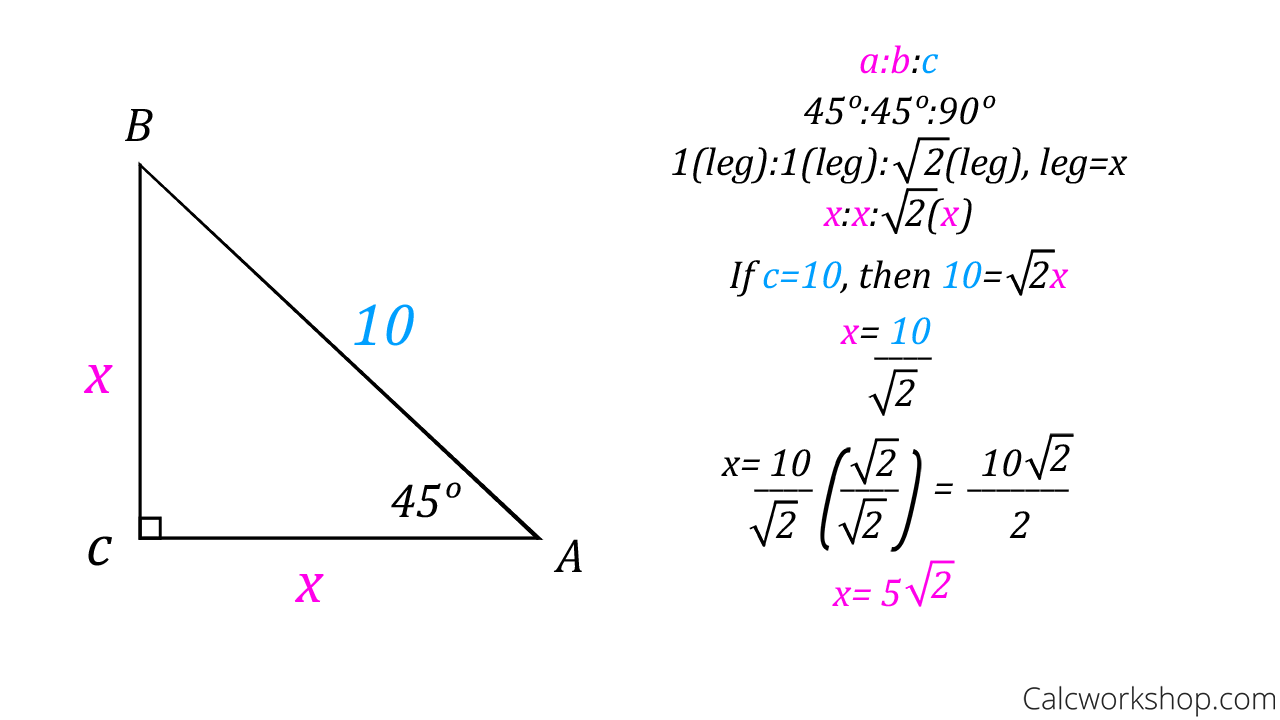



Special Right Triangles Fully Explained W 19 Examples



Special Right Triangles Proof




Special Right Triangles 30 60 90 And 45 45 90 Triangles Matter Of Math



Unit 5 Trigonometry



Day 1 Hw Special Right Triangles 45 45 90 30 60 90 Youtube



Solved I Understand That The Triangles Are 45 45 90 And 30 60 90 But I Am Getting Lost With The Triangles Together I Understand That I Need To Fi Course Hero




Amazon Com Bronagrand Triangle Ruler Square Set 30 60 And 45 90 Degrees Set Of 2 Everything Else



45 45 90 And 30 60 90 Triangles Zona Land Education



Special Right Triangles Formulas 30 60 90 And 45 45 90 Special Right Triangles Examples Pictures And Practice Problems



Special Right Triangles 30 60 90 And 45 45 90 Quiz Quizizz




Solved 1 Of 4 Trigonometry Prerequisite Special Right Chegg Com




Sat Math Multiple Choice Practice Question 17 Answer And Explanation Cracksat Net



Math Tutor Berkeley San Francisco Bay Area Mathematics Physics Algebra Geometry Trigonometry Calculus Tutoring Special Right Triangles Mayeri Education
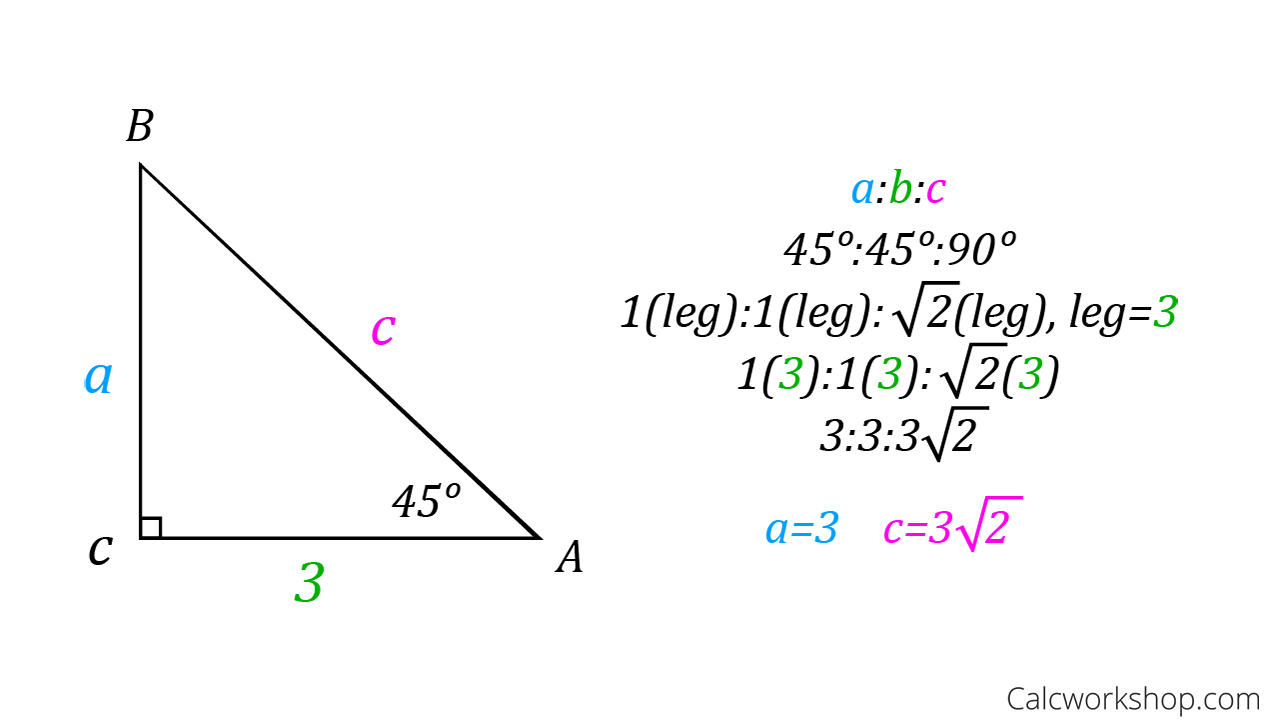



Special Right Triangles Fully Explained W 19 Examples




Right Triangles Interactive Notebook Pages Mrs E Teaches Math




Special Right Triangles Fun Group Activity 30 60 90 And 45 45 90
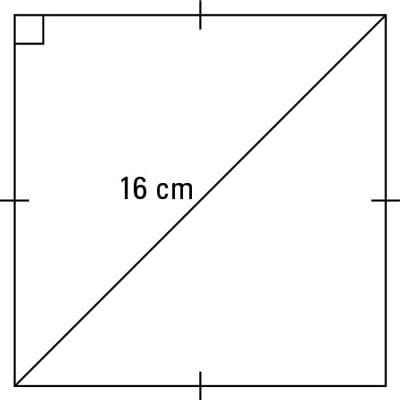



How To Work With 30 60 90 And 45 45 90 Degree Triangles Dummies




5 30 60 90 Triangles Geometry15a




Special Right Triangles Review Article Khan Academy




10 2 Special Right Triangles Learning Objective To Find Relationships Among Side Lengths In And Triangles And To Find Distances In Real Ppt Download




Amazon Com Triangle Set 10 Inch 30 60 45 90 Office Products



45 45 90 And 30 60 90 Triangles Zona Land Education



1




Special Right Triangles Part 1 45 45 90 And 30 60 90 Youtube
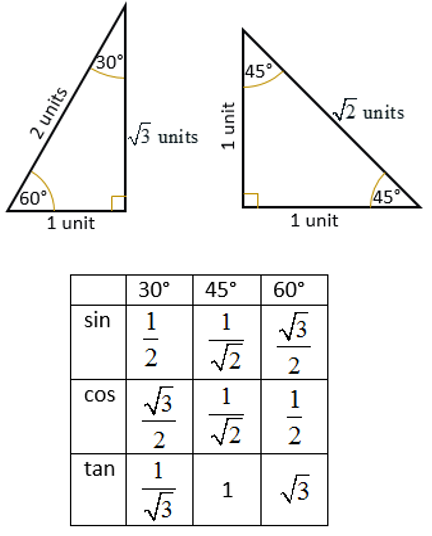



Trigonometric Ratios Of Special Angles 0 30 45 60 90 Video Lessons Examples And Solutions




How To Work With 30 60 90 And 45 45 90 Degree Triangles Dummies
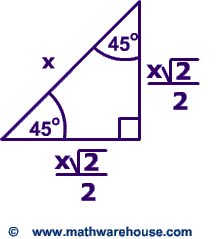



Special Right Triangles Formulas 30 60 90 And 45 45 90 Special Right Triangles Examples Pictures And Practice Problems
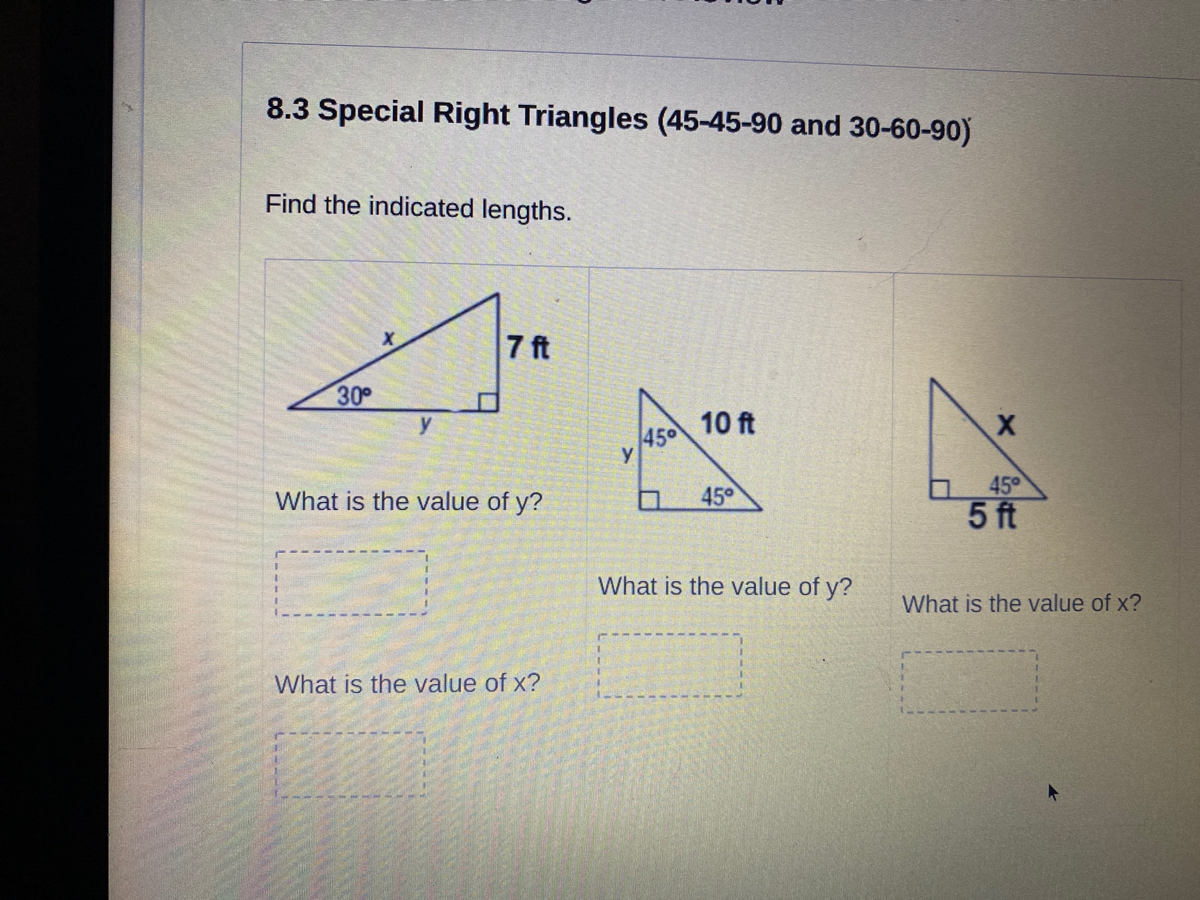



Answered 8 3 Special Right Triangles 45 45 90 Bartleby




Analyzing 45 45 90 Triangles Iheartgeo
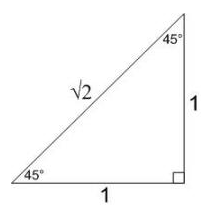



How To Use The Special Right Triangle 45 45 90 Studypug




Ideas And Resources For The Secondary Math Classroom Better Questions Special Right Triangles Teaching Geometry Right Triangle Secondary Math Classroom
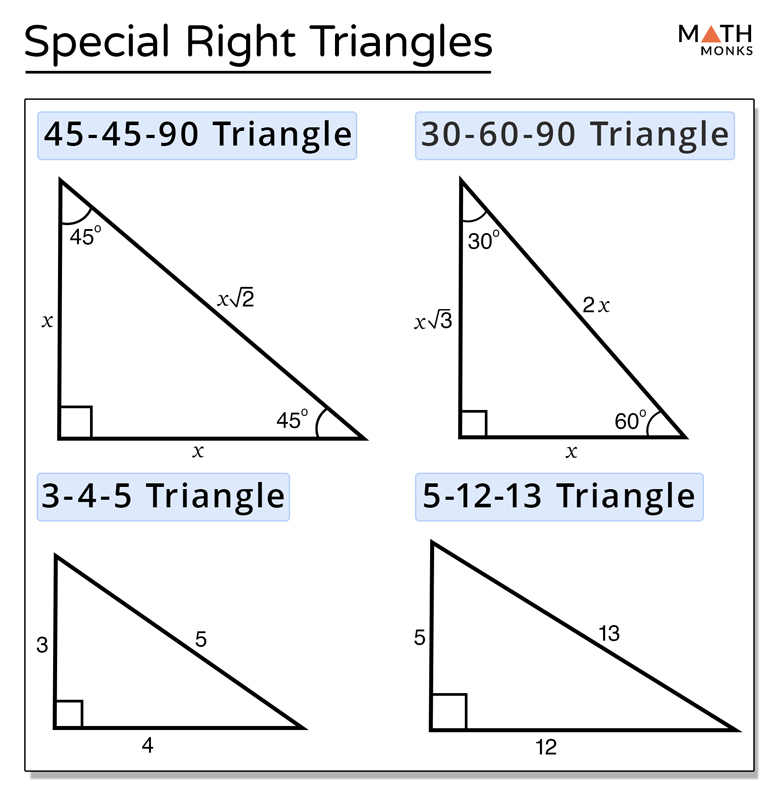



Special Right Triangles Definition Formula Examples




Fighting The War On Drugs Using Geometry And Special Triangles Real World Geometry Ck 12 Foundation




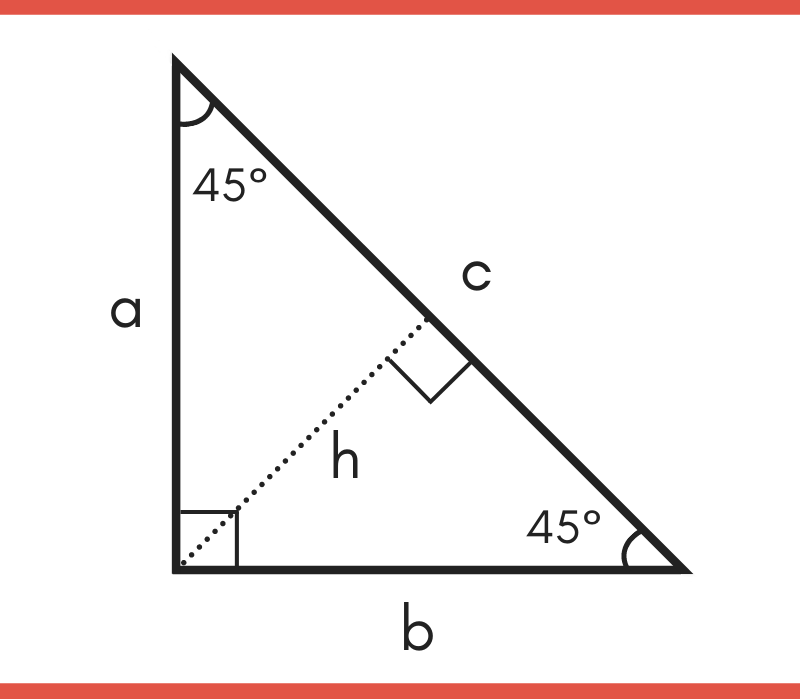
Solved U9 L4 Special Right Triangles Practice An Altitude H Chegg Com
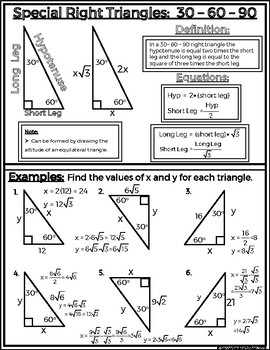



Special Right Triangles 45 45 30 60 90 Notes Sheet Graphic Organizers



30 60 90 And 45 45 90 Triangle Calculator




30 60 90 Triangle Calculator Formula Rules
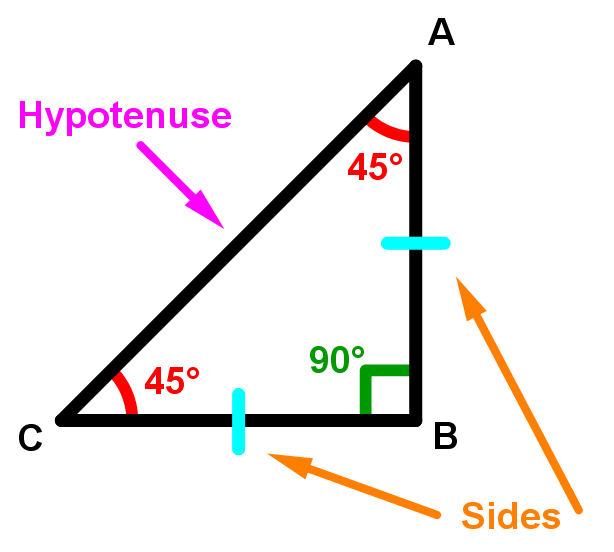



How To Use The Special Right Triangle 45 45 90 Studypug



What Are Some Differences And Similarities Between 30 60 90 Triangles And 45 45 90 Triangle Quora



Special Right Triangles Proof



Right Triangles Gmat Free




Special Angles Larger Than 90º




Special Right Triangles Review Article Khan Academy




30 60 90 Triangle Explanation Examples



Geometry Lesson 7 2 Special Right Triangles Lessons Blendspace
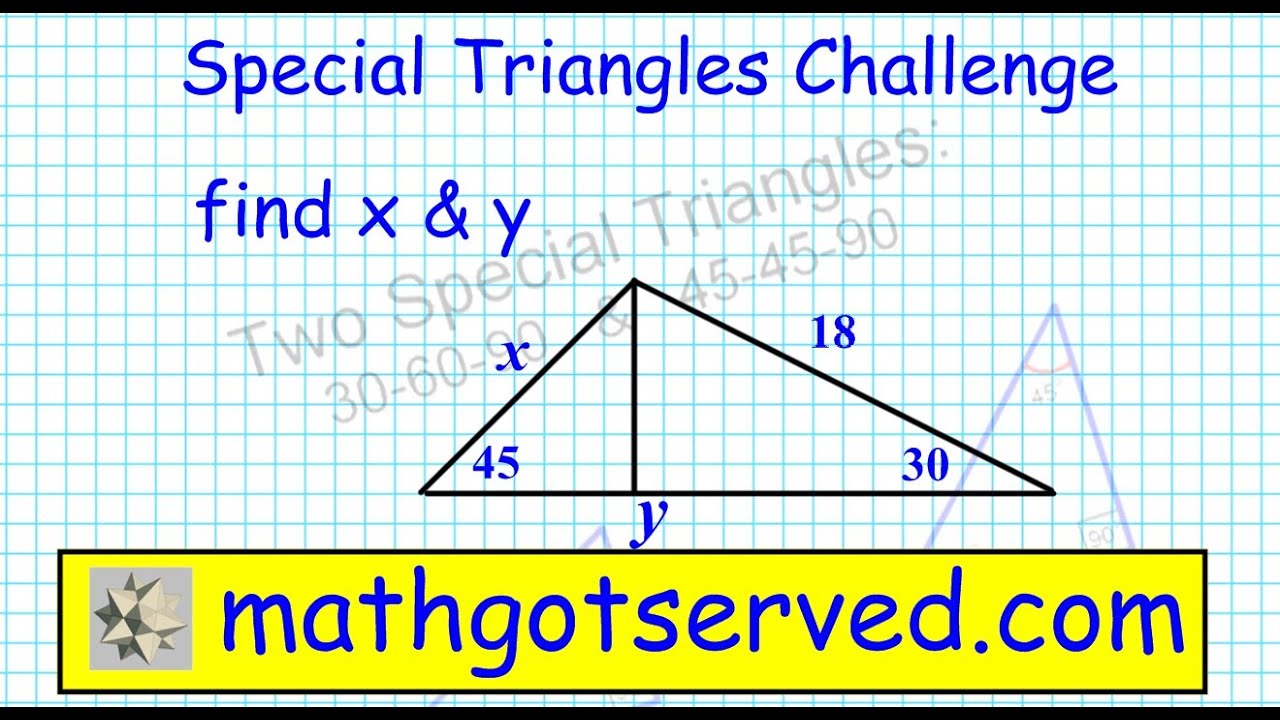



Complex Special Triangles 45 45 90 30 60 90 Similar Triangles Geometry Trig Youtube




Special Right Triangles 30 60 90 And 45 45 90 Triangles Matter Of Math



0 件のコメント:
コメントを投稿